Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://englischraum.de/vorkurszettel?id=76
| argl, Tyskie84 | www.matheraum.de Oberstufenmathematik - Analysis/Analytische Geometrie Aufgabenblatt 4 Abgabe: Fr 30.01.2009 19:00 | 30.12.2008 |
| Aufgabe 1 | ||
| Untersuchen Sie die gegenseitige Lage der Ebenen a) 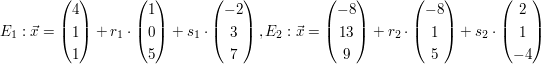 b) 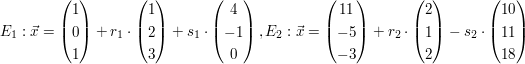 c) d) 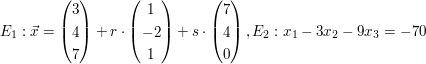 | ||
| Aufgabe 2 | ||
| Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E. Bestimme gegebenfalls den Durchstoßpunkt.
a) 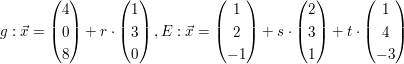 b) 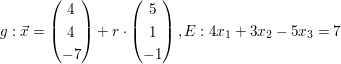 | ||
| Aufgabe 3 | ||
Gegeben sind 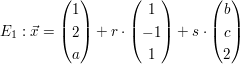 und und 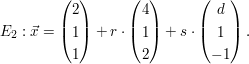 Wie müssen die reellen Zahlen Wie müssen die reellen Zahlen | ||
| Aufgabe 4 | ||
| Bestimmen Sie 1. sich schneiden 2. zueinander parallel sind und keine gemeinsamen Punkte haben 3. identisch sind a) 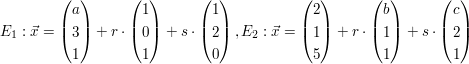 b) | ||
© Copyright 2003-25 www.englischraum.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.