KinetikReaktionskinetik
Die Reaktionskinetik (kurz Kinetik) befasst sich mit der Geschwindigkeit chemischer Reaktionen. Die Geschwindigkeit wird dabei durch die Änderung der Konzentration beschrieben. Eine Änderung wird mathematisch als Differential geschrieben.
Beispiel:
Es wird die Aenderung der Konzentration eines Stoffes A untersucht. Die Konzentration des Stoffes A wird dabei immer als [A] geschrieben. Die Aenderung der Konzentration ueber die Zeit schreibt man als ![$ \frac{d[A]}{dt} $ $ \frac{d[A]}{dt} $](/teximg/2/2/01439122.png) . Fuer das ungeuebte Auge sieht das zunaechst kompliziert aus, davon sollte man sich jedoch nicht entmutigen lassen. Ausgesprochen wuerde man sagen, die Aenderung der Konzentration des Stoffes A innerhalb eines Zeitintervalls dt. . Fuer das ungeuebte Auge sieht das zunaechst kompliziert aus, davon sollte man sich jedoch nicht entmutigen lassen. Ausgesprochen wuerde man sagen, die Aenderung der Konzentration des Stoffes A innerhalb eines Zeitintervalls dt.
Reaktion 0. Ordnung
Bei einer Reaktion 0. Ordnung reagiert ein Edukt A zu einem Produkt B. Die Reaktionsgeschwindigkeit ist dabei gänzlich unabhängig von der Konzentration von A oder B (im Unterschied zu einer Reaktion 1. Ordnung).
Die Reaktion kann wie folgt formuliet werden:
Die Änderung der Konzentration (die Konzentration wird in eckigen Klammern angegeben) von A im Zeitintervall (zum Beispiel eine Sekunde) dt kann durch folgende Differenzialgleichung beschrieben werden.
durch Trennung der Variablen und anschließende Integration kann die Gleichung folgendermaßen gelöst werden.
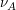 ist dabei der stöchiometrische Faktor von A, also der Faktor, mit dem A in die Reaktionsgleichung eingeht. in diesem Fall also -1. Das negative Vorzeichen ergibt sich daraus, dass A als Edukt verbraucht wird. ist dabei der stöchiometrische Faktor von A, also der Faktor, mit dem A in die Reaktionsgleichung eingeht. in diesem Fall also -1. Das negative Vorzeichen ergibt sich daraus, dass A als Edukt verbraucht wird.
Reaktion 1. Ordnung
Bei einer Reaktion erster Ordnung (häufig Zerfallsreaktionen) reagiert ein Edukt A zu einem Produkt B. Die Reaktionsgeschwindigkeit ist dabei Abhängig von der Konzentration von A bzw. B.
Die Änderung der Konzentration (die Konzentration wird in eckigen Klammern angegeben) von A im Zeitintervall (zum Beispiel eine Sekunde) dt kann durch folgende Differenzialgleichung beschrieben werden.
Die Änderung der Konzentration von A kann einmal durch die Abnahme an A oder auch durch die Zunahme von B betrachtet werden, da deren Verhältnis antiproportional ist. Solch eine Differentialgleichung wird durch Trennung der Variablen und anschließende Integration gelöst. Die Grenzen sind hierbei ![$ [A]_0 $ $ [A]_0 $](/teximg/5/2/01424125.png) zum Zeitpunkt zum Zeitpunkt 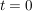 und und ![$ [A]_t $ $ [A]_t $](/teximg/6/2/01424126.png) zum Zeitpunkt t=t. zum Zeitpunkt t=t.
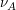 ist dabei der stöchiometrische Faktor von A, also der Faktor, mit dem A in die Reaktionsgleichung eingeht. in diesem Fall also -1. Das negative Vorzeichen ergibt sich daraus, dass A als Edukt verbraucht wird. Die Integration lässt sich für B analog durchführen, wodurch man auf folgende Lösung kommt. ist dabei der stöchiometrische Faktor von A, also der Faktor, mit dem A in die Reaktionsgleichung eingeht. in diesem Fall also -1. Das negative Vorzeichen ergibt sich daraus, dass A als Edukt verbraucht wird. Die Integration lässt sich für B analog durchführen, wodurch man auf folgende Lösung kommt.
Durch Umstellen kann die Gleichung auch als e-Funktion beschrieben werden.
Halbwertszeit einer Reaktion 1. Ordnung
Die Halbwertszeit einer Reaktion beschreibt den Punkt, ab dem die Ausgangskonzentration (hier ![$ [A]_0 $ $ [A]_0 $](/teximg/5/2/01424125.png) ) auf die Hälfte abgesunken ist. Zur Halbwertszeit ) auf die Hälfte abgesunken ist. Zur Halbwertszeit 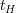 gilt also gilt also ![$ [A]_t=0,5[A]_0 $ $ [A]_t=0,5[A]_0 $](/teximg/9/4/01424149.png)
Setzt man dies in die obige Gleichung ein, so erhält man
Die Halbwertszeit einer Reaktion 1. Ordnung ist somit unabhängig von der Ausgangskonzentration und wird lediglich durch die Geschwindigkeitskonstante k beeinflusst.
Beispielaufgabe: Mumie
Bei einer Mumie wird zur Altersbestimmung die 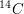 -Radioisotopmethode angewendet. Dabei wurde festgestellt, dass die Radioaktivität noch 56,2 % der Radioaktivität der lebenden Substanz beträgt. Wie alt ist die Mumie? Die Halbwertszeit des -Radioisotopmethode angewendet. Dabei wurde festgestellt, dass die Radioaktivität noch 56,2 % der Radioaktivität der lebenden Substanz beträgt. Wie alt ist die Mumie? Die Halbwertszeit des 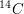 beträgt 5568 Jahre. beträgt 5568 Jahre.
Es handelt sich um eine Reaktion erster Ordnung:
1. Ermittlung von k
2. Ermittlung von t
Die Mumie ist 4629 Jahre alt.
Reaktion 2. Ordnung
Bei einer Reaktion 2. Ordnung reagieren zwei Edukte A und B zu einem (oder auch mehreren) Produkten.
Hier wird die Differentialgleichung etwas komplexer, als bei einer Reaktion 1. Ordnung.
Ist die Konzentration von A gleich der Konzentration von B kann die Differentialgleichung folgendermaßen gelöst werden.
Sind die Konzentrationen jedoch nicht gleich, so gestaltet sich die Berechnung deutlich komplizierter und Integrationskonstanten müssen mitberücksichtigt werden.
Wie gewohnt wird die Differentialgleichung aufgestellt.
Die Konzentration an A und B kann auch als Funktion des gebildeten Produktes C formuliert werden. Um später nicht mit den Integrationskonstanten durcheinander zu geraten, wird statt C x geschrieben.
Unter Verwendung der beiden Gleichungen erhält man unter Berücksichtigung der richtigen stöchiometrischen Faktoren
Trennung der Variablen ergibt dann
Um eine nachfolgende Integration zu ermöglichen bedient man sich hier der Partialbruchzerlegung.
Für die Faktoren a und b folgt
Dementsprechend kann die ursprüngliche Differentialgleichung auch wie folgt geschrieben werden
Die Integrationskonstanten 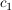 und und 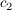 ergeben sich durch einsetzen der Randbedingungen (x=0, t=0) zu ergeben sich durch einsetzen der Randbedingungen (x=0, t=0) zu
Dementsprechend folgt
Eine typische Anwendungsaufgabe ist dabei unter anderem die Hydrolyse von Ethylacetat.
Übungsaufgabe: Dimerisierung
Die Reaktionsgeschwindigkeit der Dimerisierung von Butadien beträgt bei 305 °C 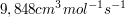 . Wie viel % Butadien sind nach 30 min dimerisiert, wenn die Anfangskonzentration 0,05 mol/L beträgt? Wie groß ist die Halbwertszeit? . Wie viel % Butadien sind nach 30 min dimerisiert, wenn die Anfangskonzentration 0,05 mol/L beträgt? Wie groß ist die Halbwertszeit?
Die Dimerisierung ist eine Reaktion 2. Ordnung. Wie bereits gezeigt wurde gilt somit
Nach 30 Minuten sind 47 % dimerisiert.
Analog zur Reaktion 1.Ordnung gilt bei 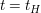 ![$ [A]=0,5[A]_0 $ $ [A]=0,5[A]_0 $](/teximg/5/7/01424775.png) , wodurch folgt , wodurch folgt
Übungsaufgabe: Reaktionszeit
Bei der Reaktion 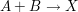 beträgt die Reaktionsgeschwindigkeitskonstante beträgt die Reaktionsgeschwindigkeitskonstante 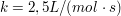 . Welche Reaktionszeit muss man ansetzen, um bei gleichen Ausgangskonzentrationen von A und B von 4 mol/L einen Umsatz vin 99,9 % zu erreichen? . Welche Reaktionszeit muss man ansetzen, um bei gleichen Ausgangskonzentrationen von A und B von 4 mol/L einen Umsatz vin 99,9 % zu erreichen?
Der Umsatz p ist wie folgt definiert:
Bei r=0,999 gilt demnach ![$ [A]=[A]_0\cdot{}0,999 $ $ [A]=[A]_0\cdot{}0,999 $](/teximg/2/9/01424792.png)
Dementsprechend folgt für die Reaktionszeit t
Man muss eine Reaktionszeit von 99,9 s ansetzen.
zurück zu
Physikalische Chemie
|