Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://englischraum.de/vorkurszettel?id=39
www.matheraum.de
Wahrscheinlichkeitstheorie (Bauer)
Aufgabenblatt 2
Abgabe: Fr 15.06.2007 10:00		18.05.2007
Dieser Übungszettel enthält die Aufgaben aus Kapitel I, § 3. Verteilung, Erwartungswert, Varianz, Jensensche Ungleichung.
Die Aufgaben sind diesmal sehr technisch, der nächste Aufgabenzettel wird wieder interessanter.
Aufgabe 1
Eine $ (\IR^d,\mathcal{B}^d) $-Zufallsvariable $ X $ auf einem W-Raum $ (\Omega,\mathcal{A},P) $ nehme nur abzählbar viele Werte $ \omega_i' $, $ i\in I $ an ($ I $ abzählbar).
Man zeige, dass

$ P_X=\summe_{i\in I} P\{X=\omega_i'\}\varepsilon_{\omega_i'} $
Aufgabe 2
Man betrachte den Laplaceschen W-Raum $ (\Omega,\mathcal{A},P) $ aus § 2, Situation 1 (b); dort ist $ \Omega=\Omega_0\times \ldots\times\Omega_0 $ das Produkt von $ m $ Kopien einer $ n $-elementigen Menge $ \Omega_0 $ (z.B. von Kugeln).
$ \Omega_0 $ sei die Vereinigung zweier fremder Teilmengen $ \Omega_0^s $ und $ \Omega_0^w $ (z.B. der Menge aller schwarzen bzw. weißen Kugeln).
Für jedes $ \omega=(\omega_1,\ldots,\omega_m) $ bezeichne $ X(\omega) $ die Anzahl aller Indizes $ i=1,\ldots,m $ mit $ \omega_i\in \Omega_0^s $.
Man bestimme die Verteilung der Zufallsvariablen $ X $.

Situation § 2, 1 (b):
In einer Urne befinden sich gut durchmischt $ n $ gleichartige Kugeln in den Farben Schwarz und Weiß, etwa $ s $ schwarze und $ w $ weiße ($ s+w=n $). Man zieht willkürlich $ m\le n $ Kugeln und legt jede gezogene Kugel sofort wieder in die Urne zurück.
Gefragt ist die Wahrscheinlichkeit, dass darunter genau $ k\le s $ schwarze Kugeln sind.
Aufgabe 3
Sei $ g:\IR\to\IR_+ $ eine symmetrisierte, Borel-meßbare, auf $ \IR_+ $ isotone Funktion mit $ g(x)>0 $ für alle $ x\not=0 $.
Ferner sei $ X $ eine reelle Zufallsvariable.
Man beweise die folgende Verallgemeinerung der MBChebyshev-Markovschen Ungleichung (vgl. MI, (20.1)):

$ P\{|X|\ge\alpha\}\le \bruch{1}{g(\alpha)}E(g(X)) $


($ \alpha>0 $)
Aufgabe 4
Es sei $ X $ eine Zufallsvariable auf $ (\Omega,\mathcal{A},P) $ mit Werten in $ \IN $.
Man beweise die Gleichheit

$ E(X)=\summe_{n=1}^\infty P\{X\ge n\} $


sowohl auf elementarem Weg als auch mit Hilfe von MI (23.10).

MI (23.10): 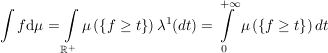$ \integral f\mathrm{d}\mu=\integral_{\IR^+} \mu\left(\left\lbrace f\ge t\right\rbrace\right)\lambda^1(dt)=\integral_{0}^{+\infty} \mu\left(\left\lbrace f\ge t\right\rbrace\right) dt $
Aufgabe 5
In der Situation des Satzes 3.8 (siehe Satz "rechtsseitige Tangenten konvexer Funktionen verlaufen unterhalb des Graphen" im MatheBank-Artikel MBkonvex) zeige man, dass für beliebige Punkte $ x,y\in \mathring{I} $ mit $ x<y $ die Ungleichungen

$ q'_{-}(x)\le q_{+}'(x)\le q_{-}(y)\le q'_+(y) $


gelten.
Aufgabe 6
Aus der MBJensenschen Ungleichung (3.23) folgere man für eine konvexe Funktion $ q $ auf einem offenen Interval $ I\subset\IR $ die folgende elementare Form dieser Ungleichung:

$ q\left(\summe_{i=1}^n \lambda_i x_i\right) \le \summe_{i=1}^n \lambda_i q(x_i) $


für je endlich viele Punkte $ x_1,\ldots,x_n\in I $ und reelle Zahlen $ \lambda_1,\ldots,\lambda_n\in\IR_+ $ mit $ \lambda_1+\ldots+\lambda_n=1 $.
Gilt diese Aussage auch, wenn $ I $ ein beliebiges Intervall und $ q $ hierauf konvex ist?
Aufgabe 7
Man beweise, dass der Satz 3.9 (=MBJensensche Ungleichung) auch für ein beliebiges Intervall $ I\subset\IR $ gültig ist.
Hierzu analysiere man das Verhalten von $ q $ in einem Endpunkt von $ I $. Insbesondere zeige man zunächst, dass eine konvexe Funktion $ q $ auf $ I $ nach unten halbstetig ist, d.h. dass für jedes $ \alpha\in\IR $ die Menge aller $ x\in I $ mit $ q(x)>\alpha $ offen in $ I $ ist.
© Copyright 2003-25 www.englischraum.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.