konvex
Schule
Definition konvex
Als konvex (lat.: convexus gewölbt, gerundet) bezeichnet man u. a. in der Mathematik und in der Optik Formen (Flächenteile, Linien), die nach außen gewölbt sind.
Gegenteil zu konkav
siehe Wikipedia
Definition konvexe Funktion
Universität
Definition konvexe Funktion
Es sei 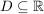 oder oder 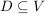 , V Vektorraum. , V Vektorraum.
Eine Funktion 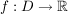 heißt konvex, wenn für alle heißt konvex, wenn für alle  mit mit 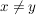 gilt: gilt:
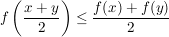
Die Funktion heißt streng konvex, wenn sogar "<" in obiger Ungleichung gilt.
Beispiele für konvexe Funktionen
1) 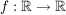 , , 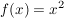 : streng konvex : streng konvex
Sätze über konvexe Funktionen
Lemma.
Dann gilt:
Dabei ist 
Quelle: isbn3110172364
Quelle: isbn3110172364
Definition konvexe Menge
Universität
|