Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| argl, Tyskie84 | www.matheraum.de
Oberstufenmathematik - Analysis/Analytische Geometrie
Aufgabenblatt 3
Abgabe: Fr 30.01.2009 19:00 | 30.12.2008 | | | | Aufgabe 1 | Untersuche Sie die gegenseitige Lage der Geraden g und h.
a) 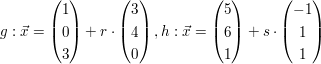
b) 
c) 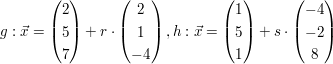 | | Aufgabe 2 |
Berechnen Sie jeweils die Relationen der Geraden g und h !
a)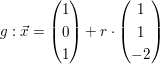 
b)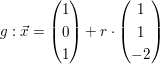 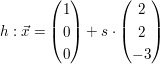
c)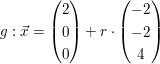 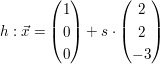
d)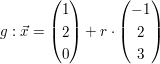 
| | Aufgabe 3 |
Bestimmen Sie jeweils die Geradengleichung der Geraden g durch die Punkte A und B bzw. die Geradengleichung der Geraden h durch die Punkte C und D und untersuchen Sie die Lage der Geraden zueinander !
a) 
b) 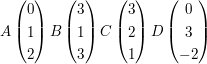
c) 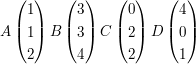
| | Aufgabe 4 |
Prüfen Sie welche Lage die Gerade 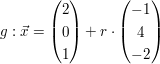 und die Gerade und die Gerade 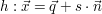 zueinander haben ! zueinander haben !
a) 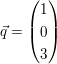 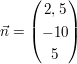
b) 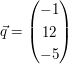 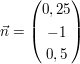
c) 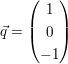 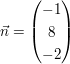
| | Aufgabe 5 |
Prüfen Sie ob der Punkt P auf der Strecke AB liegt !
a) 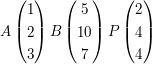
b) 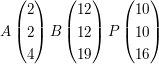
c) 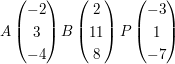
| | Aufgabe 6 |
Prüfen Sie ob sich die Gerade g durch die Punkte A und B und die
Strecke CD schneiden !
a) 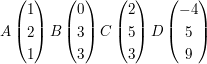
b) 
| | Aufgabe 7 |
Überprüfen Sie rechnerisch ob sich die Strecken AB und CD schneiden ! Ermitteln Sie das Teilungsverhältnis, in dem sie durch den Schittpunkt S geteilt werden !
a) 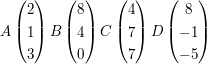
b) 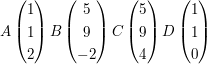
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|