Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| argl, Tyskie84 | www.matheraum.de
Oberstufenmathematik - Analysis/Analytische Geometrie
Aufgabenblatt 4
Abgabe: Fr 30.01.2009 19:00 | 30.12.2008 | | | | Aufgabe 1 | Untersuchen Sie die gegenseitige Lage der Ebenen 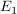 und und 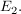 Bestimmen Sie gegebenfalls die Gleichung der Schnittgeraden. Bestimmen Sie gegebenfalls die Gleichung der Schnittgeraden.
a) 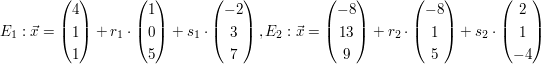
b) 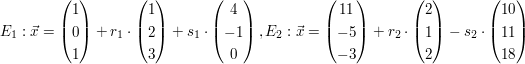
c) 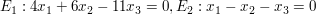
d) 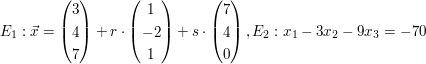 | | Aufgabe 2 | Untersuchen Sie die gegenseitige Lage der Geraden g und Ebene E. Bestimme gegebenfalls den Durchstoßpunkt.
a) 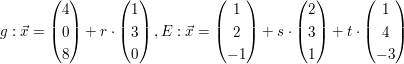
b) 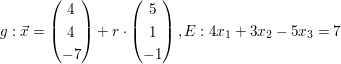 | | Aufgabe 3 | Gegeben sind 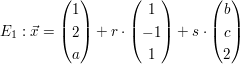 und und 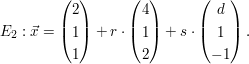 Wie müssen die reellen Zahlen Wie müssen die reellen Zahlen 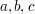 und und 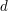 gewählt werden, damit sich die beiden Ebenen gewählt werden, damit sich die beiden Ebenen 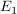 und und 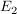 schneiden? schneiden? | | Aufgabe 4 | Bestimmen Sie 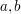 und und  so, dass die Ebenen so, dass die Ebenen 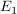 und und 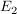
1. sich schneiden
2. zueinander parallel sind und keine gemeinsamen Punkte haben
3. identisch sind
a) 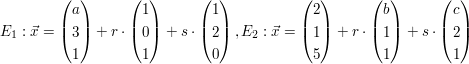
b) 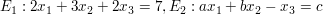 |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|