Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| argl, Tyskie84 | www.matheraum.de
Oberstufenmathematik - Analysis/Analytische Geometrie
Aufgabenblatt 7
Abgabe: Fr 01.05.2009 22:00 | 31.03.2009 | | | | Aufgabe 1 | Die Abbildung zeigt das Endstück einer Gardinenstange. Das Endstück wurde so in ein Koordinatensystem gelegt, dass es symmetrisch zur x- Achse liegt.
![[Dateianhang]](uploads/forum/00418801/forum-i00418801-n001.jpeg)
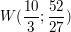 , P(0;0) und Q(5;1,5) , P(0;0) und Q(5;1,5)
1. Bestimme mithilfe der Koordinaten von P und Q sowie des Wendepunktes die Gleichung einer ganzrationalen Funktion 3. Grades 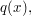 die die Querschnittsfunktion im 1. Quadranten darstellt. (Kontrolle: die die Querschnittsfunktion im 1. Quadranten darstellt. (Kontrolle: 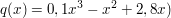
2. Die Endstücke sollen in quaderförmige Schachteln mit quadratischer Grundfläche so verpackt werden, dass das äußere Ende nach oben zeigt. Bestimme die Länge der Grundfläche der Schatel und ihr Volumen.
3. Um das Endstück auf die Gardinenstange zu stecken, befindet sich am Ende ein 3cm tiefer zylindrischer Hohlraum mit einem Durchmesser von 2,5cm. Beweisen, dass die restliche Wandstrecke das Endstück überall wenigstens 2mm dick ist.
4. Berechne den Materialverbrauch bei der Herstellung des Endstücks. Zeige zuvor, dass ![$ [\\q(x)]^{2}=0,01x^{6}-0,2x^{5}+1,56x^{4}-5,6x^{3}+7,84x^{2} $ $ [\\q(x)]^{2}=0,01x^{6}-0,2x^{5}+1,56x^{4}-5,6x^{3}+7,84x^{2} $](/teximg/2/8/00909482.png) gilt. gilt.
| | Aufgabe 2 | Gegeben ist die Funktionsschar 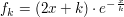 mit mit 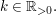
1. Gebe die Definitionsmenge an, bestimme die Schnittpunkte der Graphen mit der x-undy-Achse und untersuche das Randverhalten.
2. Bestimme die Ableitungen 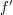 und und 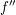 und bestimme anschließend die Lage und Art des Extremums. und bestimme anschließend die Lage und Art des Extremums.
3. Jede Funktion der Funktionsschar 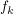 hat einen Wendepunkt an der Stelle hat einen Wendepunkt an der Stelle 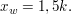 Zeige, dass die Wendetangenten aller Graphen der Schar zueinander parallel sind. Zeige, dass die Wendetangenten aller Graphen der Schar zueinander parallel sind.
4. Fertige für 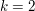 eine Skizze des Graphen der Funktion eine Skizze des Graphen der Funktion 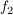 an. an.
5. Weise nach, dass die Extrempunkte aller Graphen auf einer Geraden liegen und gebe eine Gleichung dieser geraden an.
6. Die x-Achse, der Graph von 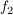 sowie die Gerade mit der Gleichung sowie die Gerade mit der Gleichung 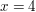 umschließt eine Fläche umschließt eine Fläche 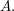 Bestimme den Flächeninhalt dieser Fläche. Zeige zunächst, dass Bestimme den Flächeninhalt dieser Fläche. Zeige zunächst, dass 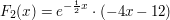 eine Stammfunktion zu eine Stammfunktion zu 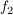 ist. ist. | | Aufgabe 3 | Gegeben ist die Funktionsschar 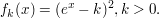
1. Diskutiere die Funktionsschar 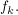 Bestimme dazu alle Nullstellen, die 1., 2. und 3. Ableitung, die Asymptoten, die Extremstellen, die Wendestellen und die Ortskurve der Wendepunkte. Bestimme dazu alle Nullstellen, die 1., 2. und 3. Ableitung, die Asymptoten, die Extremstellen, die Wendestellen und die Ortskurve der Wendepunkte.
2. Skizziere die Graphen von 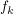 für für 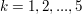 sowie die Ortskurve der Wendepunkte in einem Koordinatensystem. sowie die Ortskurve der Wendepunkte in einem Koordinatensystem.
3. Ermittle die Gleichung der Wendetangente. Diese markiert durch ihre Schnittpunkte mit der Asymptote und der x-Achse ein achsenparalles Rechteck. Bestimme die Höhe, Breite und Flächeninhalt dieses Rechteckes sowie die Koordinaten des Eckpunktes.
4. Bestimme den Inhalt des (nach links unbegrenzten) Flächenstücks 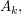 welches durch den Graphen von welches durch den Graphen von 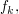 dessen Asymptote und deren Schnittpunkt mit den Graphen von dessen Asymptote und deren Schnittpunkt mit den Graphen von 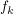 eingeschlossen wird. Vergleiche eingeschlossen wird. Vergleiche 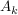 mit der Fläche des unter Teilaufgabe 3 ermittelten Rechtecks. Skizziere das Rechteck und mit der Fläche des unter Teilaufgabe 3 ermittelten Rechtecks. Skizziere das Rechteck und 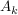 für für 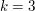 in einem Koordinatensystem. in einem Koordinatensystem. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|