Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Kurs: Kurvendiskussionen; Leiter: Adamantin | www.matheraum.de
Kurvendiskussionen
Aufgabenblatt 1
Abgabe: Mo 10.11.2008 10:00 | 20.09.2008 | | Kurvendiskussion Klasse 11 | Grenzwert, Stetigkeit, Asymptote und erste Kurven | | Aufgabe 1 | Berechne den Grenzwert für folgende Funktionen
1. 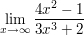
2. 
3. 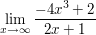
4. 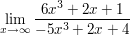
Äußere dich anschließend zur Art des Grenzwertes ("uneigentlicher Grenzwert"?) und gib eine allgemeine Regel/Vorgehensweise für die Aufgabentypen an.
| | Aufgabe 2 | Untersuche die Funktionen auf Asymptoten und Stetigkeit
1. 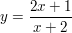
2. 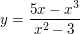
3. 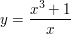 | | Aufgabe 3 | Durch welche ganzrationale Funktion können die folgenden Funktionen für betragsmäßig große x-Werte angenähert werden?
1. 
2. 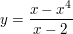
3. 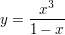
4. 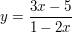
| | Aufgabe 4 |
Gegeben sei die Funktion 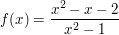
Wo ist die Funktion stetig. Kann man sie an den Definitionslücken stetig fortsetzen? | | Aufgabe 5 |
Wie lauten die Scheitelformen und Umkehrfunktionen folgender Parabelgleichungen?
a) 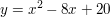
b) 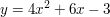
c) 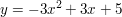 |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|