Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Kurs: Kurvendiskussionen; Leiter: Adamantin | www.matheraum.de
Kurvendiskussionen
Aufgabenblatt 2
Abgabe: Sa 08.11.2008 23:00 | 20.09.2008 | | Kurvendiskussion Klasse 11 | einfache Kurvendiskussionen, Rekonstruktion- und Extremwertaufgaben | | Aufgabe 1 |
Gegeben sei die Funktion f mit der Gleichung 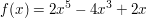
a) Wie groß ist der maximale Definitionsbereich?
b) Wie verhält sich die Funktion für x 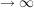 und x und x 
c) Wo liegen die Nullstellen? Gibt es mehrfache Nullstellen?
d) Bestimmen Sie ausschließlich mit Hilfe der 1. Ableitung das Steigungsverhalten und geben Sie die Extrempunkte an.
| | Aufgabe 2 | Rekonstruieren sie folgende Funktionen:
Bestimmen Sie die ganzrationale Funktion 3. Grades, die bei x=-1 eine Nullstelle hat und bei x=-2 einen Wendepunkt mit der Wendetangente y=3x+2,5.
| | Aufgabe 3 | Extremwertaufgabe:
Gegeben sei die Parabel mit der Gleichung 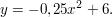
In den Ausschnitt der Ebene, der zwischen Parabel und x-Achse liegt, ist ein Rechteck
a) größten Umfangs b) größten Flächeninhalts einzubeschreiben.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|