Aufgaben zum PotenzgesetzIst 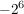 kleiner, gleich oder größer als  ?
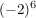Forme den Term mit Hilfe der Potenzgesetze in möglichst einfache,
gleichwertige Terme mit natürlichem Exponenten um!
![$ [x^2 \cdot{}(x\cdot{}y^3)^2]^5 $](/teximg/0/7/00388070.png "$ [x^2 \cdot{}(x\cdot{}y^3)^2]^5 $")
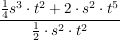
![$ \bruch{[x^2 -8x +16]^{7n+3}}{(x-4)^{5n-4}} $](/teximg/2/7/00388072.png "$ \bruch{[x^2 -8x +16]^{7n+3}}{(x-4)^{5n-4}} $")
Berechne so weit wie möglich
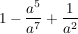
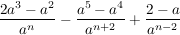
Bestimme die Lösungsmenge
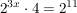
Diese Aufgaben können als Übungsaufgaben verstanden werden;
wenn du die Aufgabe gelöst hast oder noch Fragen dazu stellen möchtest,
poste die Aufgabe und deine Lösungsideen im ![[link]](/images/popup.gif "Link auf \"https://matheraum.de\"") Matheraum.
| 
