Benutzer:tobit09/Beweis-Tutorial A2Beweis-Tutorial
 2. Vorbereitungen: Definitionen 2. Vorbereitungen: Definitionen
Lösungsvorschlag Aufgabe 2
Aufgabe:
Was bedeutet die folgende Aussage? "Die Funktion 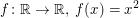 ist gerade." ist gerade."
Lösungsvorschlag:
Nach Definition bedeutet die Aussage aus der Aufgabenstellung:
Die Funktion 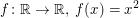 erfüllt erfüllt 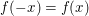 für alle reellen Zahlen für alle reellen Zahlen  . .
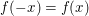 bedeutet darin wegen bedeutet darin wegen 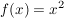 und und 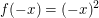 nichts Anderes als nichts Anderes als 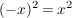 . .
Die Aussage aus der Aufgabenstellung lässt sich also auch wie folgt formulieren:
Es gilt 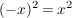 für alle reellen Zahlen für alle reellen Zahlen  . .
|