Benutzer:tobit09/Beweis-Tutorial A9Beweis-Tutorial
 3. "es existiert"-Aussagen 3. "es existiert"-Aussagen
Lösungsvorschlag Aufgabe 9
Aufgabe:
Sei  eine gerade natürliche Zahl. Zeige, dass dann auch die natürliche Zahl eine gerade natürliche Zahl. Zeige, dass dann auch die natürliche Zahl 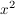 gerade ist. gerade ist.
Überlegungen zur Lösung:
Gegeben:
Natürliche Zahl  . .
 gerade, d.h. es existiert eine natürliche Zahl gerade, d.h. es existiert eine natürliche Zahl  mit mit 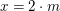 . .
Zu zeigen:
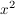 gerade, d.h. es existiert eine natürliche Zahl gerade, d.h. es existiert eine natürliche Zahl 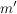 mit mit 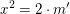 . .
Beispielsweise mit Schmierzettel-Methode ein Beispiel für 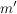 finden: finden:
1. Eine geeignete natürliche Zahl 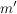 muss muss
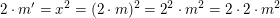
und somit 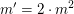 erfüllen. erfüllen.
2. Die Zahl  ist tatsächlich eine natürliche Zahl (da m eine natürliche Zahl ist) und erfüllt ist tatsächlich eine natürliche Zahl (da m eine natürliche Zahl ist) und erfüllt
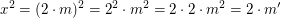 . .
Lösungsvorschlag:
Da  gerade ist, existiert eine natürliche Zahl gerade ist, existiert eine natürliche Zahl  mit mit 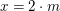 . .
Da  eine natürliche Zahl ist, ist auch eine natürliche Zahl ist, ist auch  eine natürliche Zahl. Sie erfüllt eine natürliche Zahl. Sie erfüllt
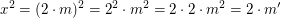 . .
Also ist 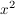 gerade. gerade.
|