Bolzano-WeierstraßSatz von Bolzano-Weierstraß
Jede beschränkte Folge in 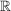 (oder (oder 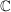 ) hat einen Häufungspunkt. ) hat einen Häufungspunkt.
Beweis für 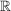
Sei 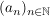 eine beschränkte Folge. Konstruiere eine Intervallschachtelung eine beschränkte Folge. Konstruiere eine Intervallschachtelung ![$ [I_k, J_k] $ $ [I_k, J_k] $](/teximg/7/5/02446157.png) , s.d. , s.d. 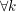 : :
Da 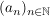 beschränkt ist, folgt beschränkt ist, folgt 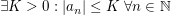 . Das impliziert für alle . Das impliziert für alle ![$ n\in\IN: a_n\in[-K,K]=:[I_1,J_1] $ $ n\in\IN: a_n\in[-K,K]=:[I_1,J_1] $](/teximg/0/6/02446160.png) . .
Sei nun ![$ [I_k,J_k] $ $ [I_k,J_k] $](/teximg/2/6/02446162.png) mit mit 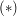 gegeben. Konstruiere dann gegeben. Konstruiere dann ![$ [I_{k+1},J_{k+1}] $ $ [I_{k+1},J_{k+1}] $](/teximg/1/6/02446161.png) wie folgt: wie folgt:
Sei 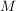 Mittelpunkt von Mittelpunkt von ![$ [I_k,J_k] $ $ [I_k,J_k] $](/teximg/2/6/02446162.png) . Dann enthält . Dann enthält ![$ [I_k,M] $ $ [I_k,M] $](/teximg/3/6/02446163.png) oder oder ![$ [M,J_k] $ $ [M,J_k] $](/teximg/4/6/02446164.png) unendlich viele unendlich viele  . Setze . Setze
Dann enthält ![$ [I_{k+1},J_{k+1}] $ $ [I_{k+1},J_{k+1}] $](/teximg/1/6/02446161.png) unendlich viele unendlich viele  und und 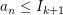 für fast alle für fast alle 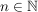 per constructionem. Für die Längen der Intervalle definiert vermöge per constructionem. Für die Längen der Intervalle definiert vermöge ![$ l:\{[a,b]|a,b\in\IR\}\to\IR $ $ l:\{[a,b]|a,b\in\IR\}\to\IR $](/teximg/1/7/02446171.png) mit mit ![$ l([a,b])=b-a $ $ l([a,b])=b-a $](/teximg/0/7/02446170.png) gilt: gilt:
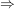 ![$ l([I_k,J_k])=\frac{1}{2^{k-1}}\cdot l([I_1,J_1]) $ $ l([I_k,J_k])=\frac{1}{2^{k-1}}\cdot l([I_1,J_1]) $](/teximg/2/7/02446172.png) 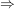 ![$ l([I_k,J_k])\to 0\mbox{ für }k\to\infty $ $ l([I_k,J_k])\to 0\mbox{ für }k\to\infty $](/teximg/3/7/02446173.png) . Also sind die . Also sind die ![$ [I_k,J_k] $ $ [I_k,J_k] $](/teximg/2/6/02446162.png) Intervallschachtellung. Intervallschachtellung.
Es existiert also ein 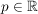 mit mit ![$ p\in[I_k,J_k]\mbox{ } \forall k\in\IN $ $ p\in[I_k,J_k]\mbox{ } \forall k\in\IN $](/teximg/7/7/02446177.png) . Zu . Zu 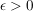 wähle wähle 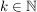 mit mit ![$ ]p-\epsilon,p+\epsilon[\supseteq[I_k,J_k] $ $ ]p-\epsilon,p+\epsilon[\supseteq[I_k,J_k] $](/teximg/8/7/02446178.png) . Da . Da ![$ [I_k,J_k] $ $ [I_k,J_k] $](/teximg/2/6/02446162.png) unendlich viele unendlich viele  enthält, folgt dies auch für enthält, folgt dies auch für ![$ ]p-\epsilon,p+\epsilon[ $ $ ]p-\epsilon,p+\epsilon[ $](/teximg/9/7/02446179.png) . Es wurde also gezeigt: . Es wurde also gezeigt:
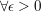 existieren unendlich viele existieren unendlich viele 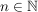 : : 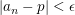 . .
Daraus folgt direkt: 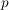 ist Häufungspunkt. ist Häufungspunkt.
(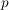 ist sogar größter Häufungspunkt! Denn existierte ein größerer Häufungspunkt, wäre ist sogar größter Häufungspunkt! Denn existierte ein größerer Häufungspunkt, wäre 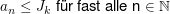 für hinreichend große für hinreichend große 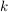 verletzt.) verletzt.)
Beispiele
Beispiel 1:
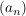 definiert durch definiert durch 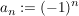 . Offensichtlich ist . Offensichtlich ist 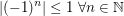 . Also hat . Also hat 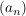 mindestens einen Häufungspunkt bzw. konvergente Teilfolgen. mindestens einen Häufungspunkt bzw. konvergente Teilfolgen.
In der Tat existieren sogar genau zwei Häufungspunkte 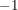 und und 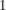 . .
Beispiel 2:
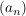 definiert durch definiert durch 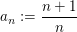 . Dann ist . Dann ist 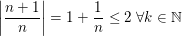 , denn , denn 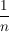 ist monoton fallend, was die Abschätzung ist monoton fallend, was die Abschätzung 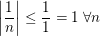 impliziert. impliziert.
Also besitzt 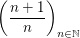 mindestens einen Häufungspunkt. mindestens einen Häufungspunkt.
Man sieht in diesem Beispiel leicht ein, dass genau ein Häufungspunkt 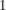 existiert. existiert.
Bemerkung
Man kann zudem folgende Formulierung des Satzes (Bolzano-Weierstraß) zeigen (vgl. dazu Amman, Escher (2006)):
Jede beschränkte Folge in 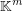 besitzt eine
konvergente Teilfolge bzw. einen Häufungspunkt. besitzt eine
konvergente Teilfolge bzw. einen Häufungspunkt.
Literatur
isbn3764377550 H. Amman/J. Escher: Analysis I
|