BruchzahlDefinition Bruch
... ist ein Ausdruck 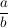 , bei dem , bei dem 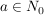 und und 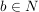 gilt. gilt.
 nennt man den Zähler des Bruches und nennt man den Zähler des Bruches und 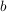 den Nenner. den Nenner.
Erweitern und Kürzen von Brüchen
Der Wert eines Bruches ändert sich nicht, wenn man Zähler und Nenner
- mit derselben natürlichen Zahl multipliziert (Erweitern)
- durch dieselbe natürliche Zahl dividiert (Kürzen)
erweitern: 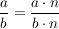 mit mit 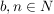
kürzen: 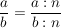 mit mit 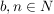
Kehrbruch
Vertauscht man bei einem Bruch Zähler und Nenner,
dann nennt man den neu entstandenen Bruch den zugehörigen Kehrbruch.
aus 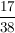 wird der Kehrbruch 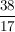
Dezimalbruch
Unter einem Dezimalbruch versteht man eine Bruchzahl, deren Nenner eine Zehnerpotenz ist:
Man schreibt: 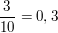 oder oder 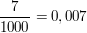 . .
===Beispiele===
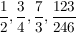
Der Nenner gibt an, in wie viele Teile ein Ganzes geteilt wird,
Der Zähler gibt an, wie viele solcher Teile für den Bruch gezählt werden.
Ist 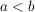 , dann nennt man den Bruch , dann nennt man den Bruch 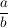 einen echten Bruch, einen echten Bruch,
ist  , dann kann man den Bruch kürzen und erhält den Wert , dann kann man den Bruch kürzen und erhält den Wert 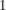 ; ;
ist 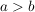 , dann nennt man den Bruch , dann nennt man den Bruch 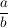 einen unechten Bruch, einen unechten Bruch,
einen unechten Bruch kann man teilweise kürzen und erhält einen gemischten Bruch:
siehe auch: Bruchterm
|