FaktorisierenMit "Faktorisieren" bezeichnet man das Umwandeln einer Summe in ein Produkt.
Dies kann durch Ausklammern eines gemeinsammen Faktor, oder durch Anwendung der binomischen Formeln geschehen.
Ausklammern
Regel:
Haben die Summanden eines Summenterms einen gemeinsammen Faktor, so kann dieser Faktor ausgeklammert werden.
Beispiele:
a) 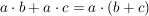
b) 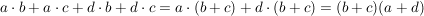
c) 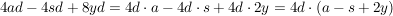
d) 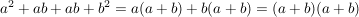
binomische Formel
Regel:
Erkennt man in einem Summenterm eine binomische Formel, kann man diese benutzen, um die Summe in ein Produkt zu verwandeln.
Beispiele:
a) 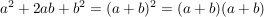
b) 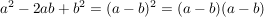
c) 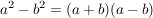
d) 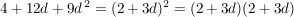
e) 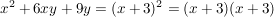
f) 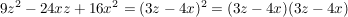
g) 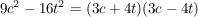
rational machen eines Nenners:
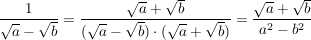
und schon sind die Wurzeln im Nenner verschwunden.
|