IntegralaufgabenBestimme die Fläche zwischen dem Graphen der Funktionen mit 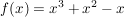 und und  . .
Die Funktion  schließt im 1. Quadranten mit der x-Achse eine Fläche von 18 FE ein. schließt im 1. Quadranten mit der x-Achse eine Fläche von 18 FE ein.
a) Welche Steigung kann eine Ursprungsgerade haben, damit sie diese Fläche schneidet?
b) Bestimme die Gleichung der Ursprungsgeraden, die von dieser Fläche ein 4,5 FE großes Teilstück oben abschneidet.
Eine Parabel 3. Ordnung geht durch  (0|0) und hat dort die Steigung 0. (0|0) und hat dort die Steigung 0.
In 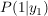 hat sie einen Wendepunkt. hat sie einen Wendepunkt.
Sie schließt mit der x- Achse für 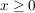 eine Fläche von eine Fläche von  FE im 4. Quadranten ein. FE im 4. Quadranten ein.
Bestimme ihre Gleichung.
Wie müssen a und b (beide >0) gewählt werden, damit die Kurve mit 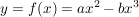 bei x=6 die x- Achse schneidet und der Inhalt der Fläche zwischen Kurve und x- Achse 18 FE beträgt? bei x=6 die x- Achse schneidet und der Inhalt der Fläche zwischen Kurve und x- Achse 18 FE beträgt?
Die Geraden mit den Gleichungen x=z und x=z+2 mit  begrenzen mit dem Graphen zu begrenzen mit dem Graphen zu 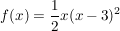 und der x-Achse einen Streifen der Breite 2 und dem Flächeninhalt A(z). und der x-Achse einen Streifen der Breite 2 und dem Flächeninhalt A(z).
Bestimmen Sie A(z) und zeigen Sie damit, dass A(0)=3 ist.
Bestimmen Sie z > 0 so, dass ebenfalls A(z)=3 gilt.
|