KompositionUnter einer Komposition (lat. compositio, "Zusammensetzung", zu componere = zusammensetzen) versteht man die "Hintereinanderausführung" oder "Verkettung" zweier oder beliebig vieler verschiedener Funktionen.
Seien f,g zwei Funktionen mit 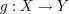 und und 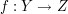 . .
Dann ist
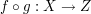 das Kompositum der Funktionen f,g. Es ist also das Kompositum der Funktionen f,g. Es ist also 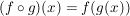 . f ist in diesem Fall die äußere Funktion und g stellt die innere Funktion dar. . f ist in diesem Fall die äußere Funktion und g stellt die innere Funktion dar.
Beispiel
Gegeben seien die Funktionen f,g mit 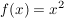 und g(x)=x+2 und g(x)=x+2
Das Kompositum 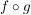 (lies: f nach g) ist (lies: f nach g) ist 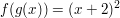
|