MaterialForum2
Die häufigsten Fragen und Antworten
![Link auf "https://matheraum.de/read?t=51425" [link]](/images/popup.gif) Wie spiegele ich eine Gerade an einer anderen? Wie spiegele ich eine Gerade an einer anderen?
![Link auf "https://matheraum.de/read?t=68677" [link]](/images/popup.gif) Wie zeige ich, dass die differenzierbaren Funktionen einen Vektorraum bilden? Wie zeige ich, dass die differenzierbaren Funktionen einen Vektorraum bilden?
![Link auf "https://matheraum.de/read?t=99792" [link]](/images/popup.gif) Geradenbüschel schneidet Ebene Geradenbüschel schneidet Ebene
![Link auf "https://matheraum.de/read?t=182943" [link]](/images/popup.gif) Wie löse ich ein Gleichungssystem mit dem Gauß-Algorithmus? Wie löse ich ein Gleichungssystem mit dem Gauß-Algorithmus?
zur gesamten Mathe-FAQ
Interessante Aufgaben
Aufgabe
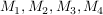 sind die Mittelpunkte der Seiten eines Vierecks sind die Mittelpunkte der Seiten eines Vierecks 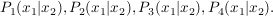
Was fällt auf, wenn man die Punkte 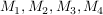 zu einem neuen Viereck verbindet? zu einem neuen Viereck verbindet?
Weise die Vermutung nach.
![Link auf "https://matheraum.de/read?t=175535" [link]](/images/popup.gif) Diskussion hier Diskussion hier
Links
![Link auf "http://members.chello.at/gut.jutta.gerhard/kurs/vektor.htm" [link]](/images/popup.gif) viele Übungsaufgaben rund um Vektoren viele Übungsaufgaben rund um Vektoren
Hier gibt es ein Java-Applet, das Lineare Gleichungssysteme löst, schrittweise veranschaulicht, mit variierbarem Tempo und beliebiger Anzahl von Gleichungen und Unbekannten: ![Link auf "https://matheraum.de/read?t=109280" [link]](/images/popup.gif) Applet Applet
Literatur |