Newton-VerfahrenNullstellenbestimmung nach dem Newton-Verfahren
Schule
Man berechnet die Nullstellen einer Funktion mit der Newton-Methode nach folgender Vorschrift:
zunächst wählt man einen Schätzwert  als Startwert, zum nächsten Näherungswert gelangt man durch folgende Rechnung: als Startwert, zum nächsten Näherungswert gelangt man durch folgende Rechnung:
Dabei ist die Wahl des Startwertes  das Diffizile. das Diffizile.
Beispiel
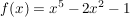
Zur Berechnung wird die Ableitung benötigt:
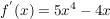
Jetzt kann man die konkrete Funktion in die allgemeinen Formel einsetzen:
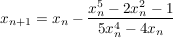
Da die Funktion mit wachsendem x hoch hinaussteigt und bei x=0 horizontal verläuft, bei x=2 > 0 ist, würde ich mal mit 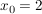 beginnen. beginnen.
Das liefert nacheinander:
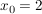
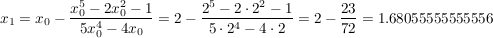
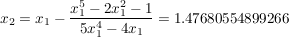

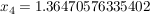
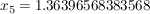
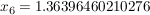
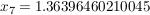
geometrische Deutung
Anschaulich kann man sich das Newtonverfahren folgendermaßen vorstellen. Man legt im Startpunkt eine Tangente an die Funktion an. Der nächste Punkt ist dann der Schnittpunkt dieser Tangenten mit der x-Achse. In diesem Punkt legt man wieder eine Tangente an die Funktion usw.
Anhand der Funktion 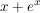 sei dies graphisch dargestellt. Die blauen Linien sind die entsprechenden Tangenten. Die Grünen markieren den entsprechenden Iterationspunkt. sei dies graphisch dargestellt. Die blauen Linien sind die entsprechenden Tangenten. Die Grünen markieren den entsprechenden Iterationspunkt.
{picture file=img/wiki_up//Newton2.jpeg}
Universität
Algorithmus (Newton-Interation)
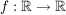 stetig differenzierbar stetig differenzierbar- f streng monoton (also
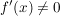 für für 
iteration:
Algorithmus (Vereinfachtes Newton-Verfahren)
![$ f:[a,b]\to\IR $ $ f:[a,b]\to\IR $](/teximg/2/1/00010612.png) stetig differenzierbar stetig differenzierbar- f streng monoton
- f(a)f(b)<0
Iteration:
Algorithmus (für zweifache Nullstellen)
Iteration:
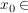 ? ?
|