Poisson-VerteilungDefinition Poisson-Verteilung
Schule
Eine Zufallsvariable X heißt Poisson-verteilt zum Parameter 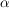 , , 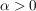 , wenn , wenn
für alle 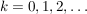
Siehe auch ![Link auf "http://de.wikipedia.org/wiki/Poisson-Verteilung" [link]](/images/popup.gif) Wikipedia Wikipedia
Universität
Für jedes 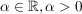 definiert definiert
eine diskrete Verteilung auf 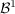 . Man nennt . Man nennt 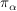 Poisson-Verteilung zum Parameter Poisson-Verteilung zum Parameter 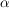 . .
Für eine Poisson-verteilte Zufallsvariable X gilt:
Beweis.
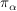 ist eine Wahrscheinlichkeitsverteilung, da ist eine Wahrscheinlichkeitsverteilung, da 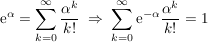 für für 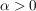
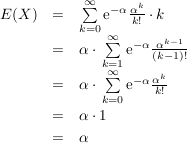
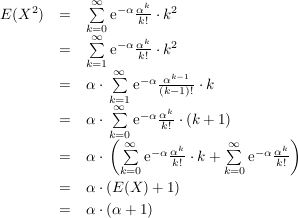
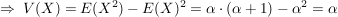
Literatur
isbn3110172364
|