TeilfolgeGegeben seien eine Menge 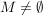 und eine Abbildung und eine Abbildung 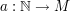 - auch notiert und bezeichnet als Folge - auch notiert und bezeichnet als Folge 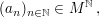 wobei wie üblich wobei wie üblich 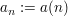 ( (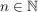 ) notiert werde. Wir sagen, dass ) notiert werde. Wir sagen, dass 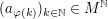 eine Teilfolge von eine Teilfolge von 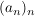 ist, falls ist, falls 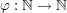 eine streng monoton wachsende Abbildung ist. eine streng monoton wachsende Abbildung ist.
Oft notiert man 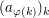 auch als auch als 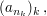 und in dieser Notation ist dann und in dieser Notation ist dann  für alle für alle 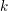 zu lesen. zu lesen.
Beispiele:
 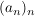 ist Teilfolge von sich selbst, da durch ist Teilfolge von sich selbst, da durch 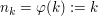 eine streng monoton wachsende Abbildung eine streng monoton wachsende Abbildung 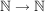 gegeben ist. gegeben ist.
 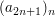 ist Teilfolge von ist Teilfolge von 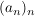 , da durch , da durch 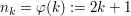 eine streng monoton wachsende Abbildung eine streng monoton wachsende Abbildung 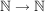 gegeben ist. gegeben ist.
 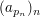 - wobei - wobei 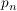 die die 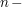 te Primzahl sei, ist Teilfolge von te Primzahl sei, ist Teilfolge von 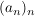 , da durch , da durch 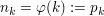 eine streng monoton wachsende Abbildung eine streng monoton wachsende Abbildung 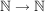 gegeben ist. gegeben ist.
|