TeleskopverknüpfungEs sei 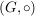 eine abelsche Gruppe - dabei sei eine abelsche Gruppe - dabei sei 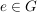 das neutrale Element und das neutrale Element und 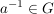 das zu das zu 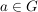 inverse Element: inverse Element: 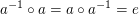 . Für Elemente . Für Elemente  definieren wir für definieren wir für 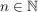
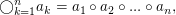
wobei hier wegen der Assoziativität auf Klammern rechterhand verzichtet wurde. Wegen der Kommutativität gilt ferner
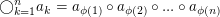
für jede Bijektion 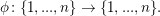 (Grob: Bei "endlichen" Verknüpfungsgebilden darf "Reihenfolge" vertauscht werden.) (Grob: Bei "endlichen" Verknüpfungsgebilden darf "Reihenfolge" vertauscht werden.)
Unter einer Teleskopverknüpfung versteht man einen Term der Form
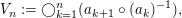
Es gilt
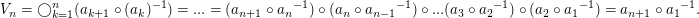
(Siehe auch: Teleskopsumme.)
|