TransformationsformelDie Transformationsformel
Beschreibung
Gegeben sei die Darstellungsmatrix 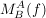 einer linearen Abbildung f von den Vektorräumen V nach W einer linearen Abbildung f von den Vektorräumen V nach W
und gesucht ist die Darstellungsmatrix 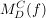 . .
Wobei A und C Basen von V und B und D Basen von W sind.
Transformationsformel
Es gilt 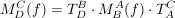 , wobei , wobei 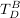 und und 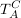 Transformationsmatrizen sind. Transformationsmatrizen sind.
Erläuterung
Wenn man ganz rechts einen Vektor v in Basisdarstellung C "hineinsteckt", wird dieser durch 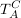 einfach nur in Basisdarstellung A gewandelt (es bleibt derselbe Vektor nur zu einer anderen Basis). einfach nur in Basisdarstellung A gewandelt (es bleibt derselbe Vektor nur zu einer anderen Basis).
Sei 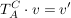
v' ist in Basisdarstellung A und kommt nun an die Darstellungsmatrix 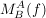 , d.h. aus v' wird , d.h. aus v' wird 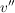 wobei wobei 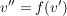 und zusätzlich in Basisdarstellung B ist. und zusätzlich in Basisdarstellung B ist.
Letztlich wird 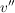 durch durch 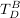 noch in Basisdarstellung D gewandelt. noch in Basisdarstellung D gewandelt.
D.H insgesamt haben wir eine Abbildung, die einen Vektor bzgl Basis C durch f abbildet und bzgl Basis D ausgibt,
also gerade 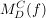
Es gilt also nur 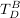 und und 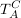 zu bestimmen und das Produkt dann auszurechnen. zu bestimmen und das Produkt dann auszurechnen.
einfachere Spezialfälle
Es gibt Situationen, wo man obige Notation vereinfachen kann:
1)
Die darstellende Matrix von f ist gegeben bzgl einer Basis A, also 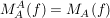 . .
Und gesucht ist die darstellende Matrix bzgl einer Basis B, also 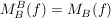
Dann muss man nur 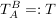 und und 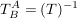 bestimmen und das Produkt wie oben entsprechend ausrechnen. bestimmen und das Produkt wie oben entsprechend ausrechnen.
(denn 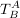 soll ja als Abbildung gerade das inverse von soll ja als Abbildung gerade das inverse von 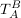 machen - siehe auch Beispiel unten) machen - siehe auch Beispiel unten)
2)
Wie eben ist 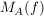 gegeben und gesucht ist gegeben und gesucht ist 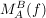 , d.h man muss nur , d.h man muss nur 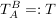 bestimmen und bestimmen und 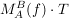 ausrechnen, denn die Rücktransformation in Basisgestalt B entfällt. ausrechnen, denn die Rücktransformation in Basisgestalt B entfällt.
3) man soll eine Koordinatentransformation berechnen.
einfaches Beispiel
gegeben sei die lin. Abbildung f durch : 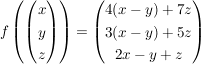
dann ist 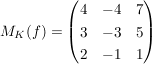 die darstellende Matrix bzgl. der kanonischen Basis die darstellende Matrix bzgl. der kanonischen Basis 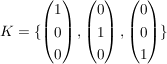
(die Bilder der Basisvektoren 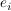 von K sind die Spalten der darstellenden Matrix von K sind die Spalten der darstellenden Matrix 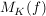 ) )
gesucht ist nun die darstellende Matrix zur Basis 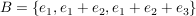
(Basisvektoren aus B sind gegeben als Linearkombinationen der Basisvektoren aus K)
also : ausrechnen von 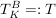 : :
wenn man den i-ten Basisvektor von B in Basisgestalt B in T reinsteckt, soll der selbe Vektor in Basisgestalt K rauskommen, also wenn man zum Beispiel  reinsteckt (dies ist der zweite Basisvektor bzgl Darstellung B) reinsteckt (dies ist der zweite Basisvektor bzgl Darstellung B)
dann soll  rauskommen, denn dies entspricht ja gerade rauskommen, denn dies entspricht ja gerade 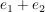 . .
Also ist 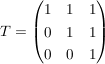 und demnach und demnach 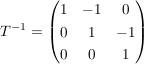
(Berechnet schnell nach Gauß-Jordan )
Deshalb ist nun 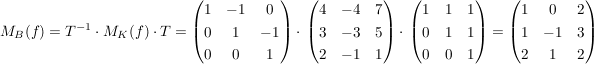
Matheraum Links
![Link auf "https://matheraum.de/read?t=77445&v=t" [link]](/images/popup.gif) ein Beispiel ein Beispiel
![Link auf "https://matheraum.de/read?t=205566" [link]](/images/popup.gif) noch ein Beispiel mit Erklärung zum ersten Spezialfall noch ein Beispiel mit Erklärung zum ersten Spezialfall
![Link auf "http://www.matheplanet.com/matheplanet/nuke/html/article.php?sid=581" [link]](/images/popup.gif) guter Artikel (MathePlanet) guter Artikel (MathePlanet)
|