UntervektorraumDefinition (Untervektorraum):
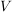 sei ein sei ein 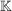 -Vektorraum. Eine Teilmenge -Vektorraum. Eine Teilmenge 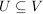 heißt Untervektorraum, falls gilt: heißt Untervektorraum, falls gilt:
(I) 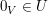
(Der Nullvektor ist Element von 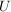 .) .)
(II) 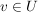 und und 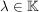 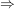 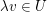 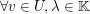 . .
(Ist  in in 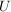 , so auch alle Vielfachen.) , so auch alle Vielfachen.)
(III)  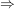 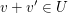 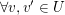 . .
(Zu zwei Vektoren in 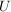 ist auch deren Summe in ist auch deren Summe in 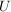 .) .)
Beispiele:
(1.) Ein sehr kleiner Untervektorraum:
 und und 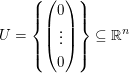 . .
Beweis:
(I) 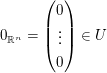
(II) 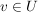 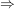 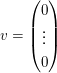 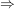 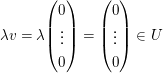 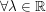
(III)  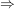 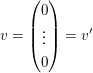 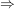 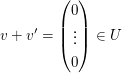 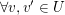 
(2.) 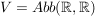 und und 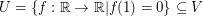 ist ein Untervektorraum. ist ein Untervektorraum.
Beweis:
(I) 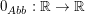 mit mit 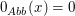 ist die Nullabbildung. ist die Nullabbildung. 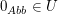 , denn , denn 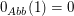 . .
(II)  , d.h. , d.h. 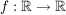 mit mit  , und , und 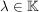 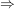 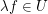 , denn , denn 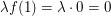 . .
(III) 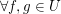 , d.h. , d.h.  mit mit  und und  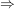 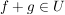 , denn , denn 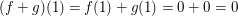 . . 
Dagegen ist 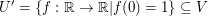 kein Untervektorraum, da (I) offensichtlich nicht erfüllt ist. kein Untervektorraum, da (I) offensichtlich nicht erfüllt ist.
(3.) Sei V ein 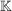 -Vektorraum. Der Spann der Vektoren -Vektorraum. Der Spann der Vektoren  , ,
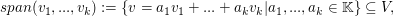
ist ein Untervektorraum.
Beweis:
(I) 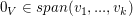 , denn , denn 
(II)  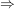 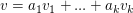 für gewisse für gewisse  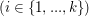 . .
 und und 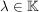 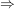 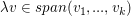 , d.h. , d.h.  für gewisse für gewisse 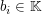 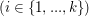 , denn: , denn:
 . Setze . Setze  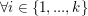 . .
(III)  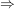 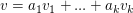 und und  für gewisse für gewisse  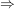  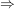  
|