VektorrechnungEin Vektor ist ein Tripel aus reellen Zahlen: 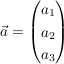
Ein Vektor enthält die Komponenten  . .
Schule
Addition und Subtraktion
Addition und Subtraktion sind also komponentenweise definiert.
Skalare Multiplikation
Ein Vektor kann mit einer reellen Zahl multipliziert werden, also vervielfacht werden:
Die skalare Multiplikation ist ebenfalls komponentenweise definiert.
Das Skalarprodukt zweier Vektoren
Das Ergebnis des Skalarprodukts ist also eine reelle Zahl.
Mulitpliziert man einen Vektor skalar mit sich selbst, so ergibt sich:
Nach dem Satz des Pythagoras berechnet man damit (in einem euklidischen Raum), nachdem man die Wurzel gezogen hat, die Länge des zu diesem Vektor gehörenden Pfeils:
Vektorprodukt
Unter dem Vektorprodukt (Kreuzprodukt) 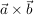 zweier Vektoren zweier Vektoren 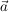 und und 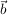 versteht man denjenigen Vektor versteht man denjenigen Vektor 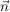 , der auf beiden Vektoren senkrecht steht. , der auf beiden Vektoren senkrecht steht.
Dabei ist die Reihenfolge zu beachten, d.h. das Vektorprodukt ist nicht kommutativ:
Für eine Übersicht klicke man auf folgende Adressen:
![Link auf "http://delphi.zsg-rottenburg.de/la1.html" [link]](/images/popup.gif) ZSG Rottenburg viele Aufgaben mit Lösungen ZSG Rottenburg viele Aufgaben mit Lösungen
![Link auf "http://www.gnoerich.de/formelsammlung/k2.html" [link]](/images/popup.gif) Private Formelsammlung Höhere Mathematik (:wink:) Private Formelsammlung Höhere Mathematik (:wink:)
|