Wie man den Kern einer linearen Abbildung bestimmtGegeben sei eine lineare Abbildung 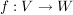 mit mit 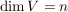 und und 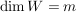 . .
Der Kern einer Abbildung ist ja die Menge aller Vektoren aus V, die auf den Nullvektor 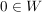 abgebildet werden: abgebildet werden:

Hat man bereits die beschreibende Matrix A dieser linearer Abbildung vorliegen (dies ist eine 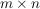 -Matrix -Matrix 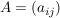 (bzgl. einer geeigneten Basis), für die gilt: (bzgl. einer geeigneten Basis), für die gilt: 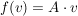 für alle für alle 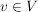 ), so reduziert sich die Bestimmung des Kerns auf das Lösen eines linearen Gleichungssystems: ), so reduziert sich die Bestimmung des Kerns auf das Lösen eines linearen Gleichungssystems:
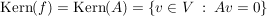
Das heißt, die Lösungsmenge dieses (homogenen) linearen Gleichungssystems ist zu bestimmen:
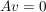
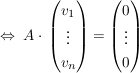

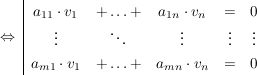
Beispiele
1. Beispiel die Telefonmatrix von 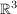 nach nach 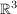 : :
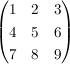
Sie hat den Rang 2 daraus bzw. aus der Dimensionsformel, lässt sich schliessen, dass es auch einen Kern gibt.
Erstellt man ein Gleichungssystem mit obigen Schema kommt man auf:
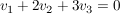
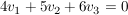
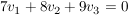
komplett aufgelöst sieht es so aus:
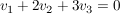
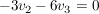
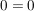
Es gibt einen Freiheitsgrad, da wir 2 Gleichungen mit 3 Unbekannten haben.
In diesem Fall setzen wir 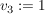 . .
Daraus folgt:
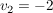
weiterhin folgt:
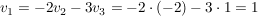 . .
Also ist der Kern:
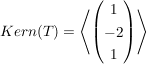
2. Beispiel:
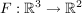 (von (von 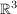 nach nach 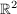 ) )
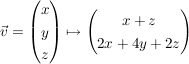
Die dazu aufgestellte Matrix lautet:
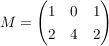
Nun können wir 2 Gleichungen aufstellen (da nach 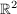 abbilden). abbilden).
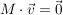
I. 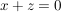
II. 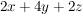
Nun wird umgeformt:
I. 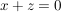
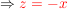

Jetzt wird II. umgeformt und I. 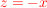 eingesetzt: eingesetzt:

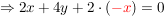
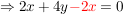

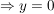
Jetzt wird II. umgeformt:

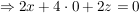
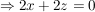
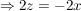
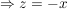
Jetzt wird I. 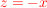 und II. und II. 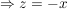 gleichgesetzt: gleichgesetzt:
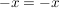

Der Kern lautet also:
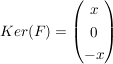
|