Wurzel AbleitungBilden Sie die Ableitungsfunktion f' der Wurzelfunktion 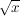 nur unter Benutzung der Definition des Differentialquotienten. nur unter Benutzung der Definition des Differentialquotienten.
Du kennst den Differentialquotienten:
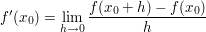
Hier 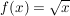
Also:
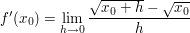
Für die Umformungen, deren Ziel es ist, h=0 einsetzen zu können (also es aus dem Nenner zu entfernen), lasse ich mal den Limes weg.
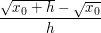
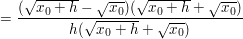
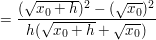
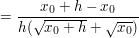
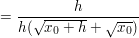
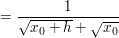
Jetzt kannst du, ohne dass der Nenner Null wird, h=0 setzen, also:
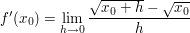
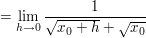
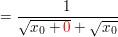
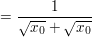
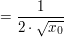
|