algebraische StrukturDefinition algebraische Struktur
Schule
Universität
Es seien 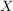 und und 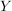 Mengen. Mengen.
Eine Abbildung
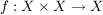
heißt eine innere Verknüpfung (oder eine innere Komposition) auf  . .
Eine Abbildung
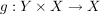
heißt eine äußere Verknüpfung (oder äußere Komposition) auf 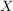 mit Operatorenbereich mit Operatorenbereich 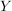 . .
Ein Tupel
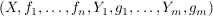
bestehend aus einer nichtleeren Menge 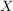 , inneren Verknüpfungen , inneren Verknüpfungen 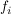 auf auf 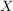 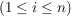 und äußeren Verknüpfungen und äußeren Verknüpfungen 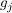 auf auf 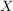 mit nichtleerem Operatorenbereich mit nichtleerem Operatorenbereich 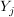 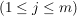 heißt eine algebraische Struktur. heißt eine algebraische Struktur.
Bemerkung
Der Begriff "algebraische Struktur" ist so weitläufig gefasst (in der Definition kann sogar 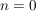 oder oder 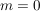 sein), dass man damit natürlich noch nicht viel anfangen kann. Es werden aber im weiteren Verlauf der Algebra recht konkrete zusätzliche Forderungen an die Verknüpfungen gestellt. sein), dass man damit natürlich noch nicht viel anfangen kann. Es werden aber im weiteren Verlauf der Algebra recht konkrete zusätzliche Forderungen an die Verknüpfungen gestellt.
Man vereinbart eine einfache Schreibweise:
Ist 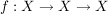 eine innere Veknüpfung auf eine innere Veknüpfung auf 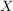 , dann bezeichnet man das , dann bezeichnet man das 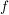 -Bild von -Bild von 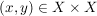 mit mit 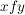 . .
In diesem Zusammenhang ist es üblich die Abbildungen nicht mit 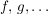 zu bezeichnen, sondern mit zu bezeichnen, sondern mit 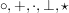 , oder ähnlich. Diese Zeichen, die Verknüpfungssymbole, sind also Bezeichnungen für innere oder äußere Verknüpfungen. , oder ähnlich. Diese Zeichen, die Verknüpfungssymbole, sind also Bezeichnungen für innere oder äußere Verknüpfungen.
Die am häufigsten verwendete Bezeichnung einer Verknüpfung 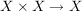 ist der Punkt, also: ist der Punkt, also:
![$ \cdot \, : \, \begin{array}{ccc} X \times X & \to & X\\[5pt] (x,y) & \mapsto & x \cdot y, \end{array} $ $ \cdot \, : \, \begin{array}{ccc} X \times X & \to & X\\[5pt] (x,y) & \mapsto & x \cdot y, \end{array} $](/teximg/9/8/00393789.png)
und das Zeichen 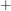 , ,
![$ + \, : \, \begin{array}{ccc} X \times X & \to & X\\[5pt] (x,y) & \mapsto & x + y. \end{array} $ $ + \, : \, \begin{array}{ccc} X \times X & \to & X\\[5pt] (x,y) & \mapsto & x + y. \end{array} $](/teximg/0/9/00393790.png)
Auch ist es üblich, in unmissverständlichenen Zusammanhängen den Punkt einfch wegzulassen und man schreibt vereinfacht 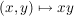 . .
In der Benennung übernimmt man die Namen, die für die Symbole in den Spezialfällen bereits festgelegt sind. So heißt 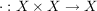 ein Produkt auf ein Produkt auf 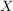 , , 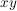 das Produkt aus den Faktoren das Produkt aus den Faktoren  und und 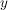 (in dieser Reihenfolge). (in dieser Reihenfolge). 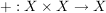 heißt Addition __auf heißt Addition __auf 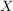 und und 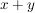 die __Summe der Summanden die __Summe der Summanden  und und 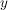 , etc. Ansonsten kann man die Bezeichnungen nach Belieben benennen, z.B. , etc. Ansonsten kann man die Bezeichnungen nach Belieben benennen, z.B.  "Kringel", "Kringel",  "Stern", etc. Will man sich nicht festlegen, liest man "Stern", etc. Will man sich nicht festlegen, liest man 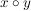 als " als " verknüpft mit verknüpft mit 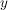 ". ".
Beispiele
a) Auf 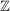 sind sind 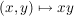 und und 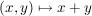 (übliche Multiplikation und Addition) innere Verknüpfungen. Aber auch (übliche Multiplikation und Addition) innere Verknüpfungen. Aber auch 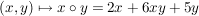 ist eine innere Verknüpfung auf ist eine innere Verknüpfung auf 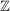 , jedoch , jedoch 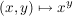 ist keine Verknüpfung auf ist keine Verknüpfung auf 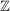 , denn i.a. ist , denn i.a. ist 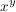 nicht in nicht in 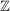 . .
b) Auf der Potenzmenge 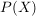 eine Menge eine Menge 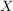 sind sind 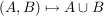 und und 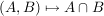 innere Verknüpfungen. innere Verknüpfungen.
c) Ist 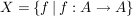 die Menge aller abbildungen von die Menge aller abbildungen von 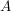 in sich und in sich und 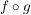 das Kompositum der Abbildungen das Kompositum der Abbildungen 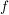 und und 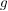 , , 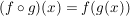 , dann ist , dann ist 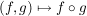 eine innere Verknüpfung auf eine innere Verknüpfung auf  . .
d) Für reelle Zahlen  und natürliche Zahlen und natürliche Zahlen  sind sind 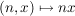 und und 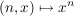 äußere Verknüpfungen auf äußere Verknüpfungen auf 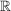 mit Operatorenbereich mit Operatorenbereich 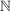 . .
Bemerkung (Verknüpfungstafeln)
Eine Verknüpfung  auf einer endlichen Menge auf einer endlichen Menge 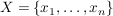 gibt man meist explizit an. Dies geschieht zweckmäßigerweise in Form der Verknüpfungtafel (für gibt man meist explizit an. Dies geschieht zweckmäßigerweise in Form der Verknüpfungtafel (für  ). Man schreibt die Elemente von ). Man schreibt die Elemente von 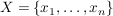 an den oberen und an den linken Rand der Tafel und ganz links oben an die Ecke das Verknüpfungszeichen. Im Schnittpunkt der an den oberen und an den linken Rand der Tafel und ganz links oben an die Ecke das Verknüpfungszeichen. Im Schnittpunkt der 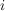 -ten Zeile und der -ten Zeile und der 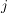 -ten Spalte ( -ten Spalte (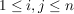 ) steht dann das Element ) steht dann das Element 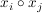 . (Die Ränder werden gelegentlich als nullte Zeile bzw. nullte Spalte bezeichnet.) . (Die Ränder werden gelegentlich als nullte Zeile bzw. nullte Spalte bezeichnet.)
Entsprechend gibt man eine Verknüpfungstafel einer äußeren Verknüpfung 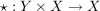 mit endlichen Mengen mit endlichen Mengen 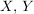 an. Jede innere Verknüpfung auf an. Jede innere Verknüpfung auf 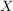 kann natürlich auch als äußere Verknüpfung auf kann natürlich auch als äußere Verknüpfung auf 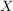 mit Operatorenbereich mit Operatorenbereich 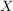 angesehen werden. Die unterschiedliche Bewertung dieser Auffassung tritt erst zutage, wenn durch zusätzliche Forderungen an eine algebraische Struktur die inneren und äußeren Verknüpfungen unterschiedlich behandelt werden. angesehen werden. Die unterschiedliche Bewertung dieser Auffassung tritt erst zutage, wenn durch zusätzliche Forderungen an eine algebraische Struktur die inneren und äußeren Verknüpfungen unterschiedlich behandelt werden.
Quelle: K. Meyberg, Algebra Teil 1, Carl Hanser Verlag, 1980, ISBN 3-446-13079-9
|