binomischer Lehrsatz
Die allgemeine Binomische Formel
Die binomische Formel ist nur ein Spezialfall des sogenannten Binomischen Lehrsatzes oder auch der allgemeinen Binomischen Formel.
Mit ihr ist es möglich, den Term
relativ leicht auszumultiplizieren.
Sie lautet:
Die Herleitung
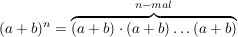
Wollen wir diese  Klammern ausmultiplizieren, so können wir bei jeder von ihnen zwischen Klammern ausmultiplizieren, so können wir bei jeder von ihnen zwischen  und und 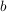 wählen. Wenn wir für alle wählen. Wenn wir für alle  Klammern entweder Klammern entweder  oder oder 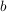 gewählt haben, so erhalten wir den Term gewählt haben, so erhalten wir den Term 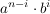 - das - das 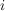 bedeutet, dass wir bedeutet, dass wir 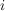 mal mal 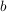 , und , und 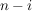 mal mal  gewählt haben. gewählt haben.
Es bleibt nun noch zu überlegen, wie viele Möglichkeiten es gibt, genau 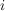 mal mal 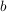 und und 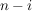 mal mal  zu wählen. Diese Anzahl liefert der Binomialkoeffizient zu wählen. Diese Anzahl liefert der Binomialkoeffizient 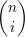 . Er gibt bekanntlich die Anzahl der Möglichkeiten an, . Er gibt bekanntlich die Anzahl der Möglichkeiten an, 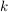 aus aus  Objekten auszuwählen. Objekten auszuwählen. 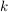 ist in diesem Falle ist in diesem Falle 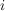 und und  ist die Anzahl der Klammern. D.h. also er gibt an, wie viele Möglichkeiten es gibt, ist die Anzahl der Klammern. D.h. also er gibt an, wie viele Möglichkeiten es gibt, 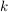 aus den aus den  Klammern auszuwählen, in denen wir Klammern auszuwählen, in denen wir 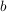 wählen. (Das ist äquivalent zu wählen. (Das ist äquivalent zu 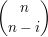 , da die Binomialkoeffizienten symmetrisch sind). , da die Binomialkoeffizienten symmetrisch sind).
Damit ist der Satz auch schon fast erklärt, fehlt nur noch die Aufsummierung aller Werte für ![$ i\in [0;n] $ $ i\in [0;n] $](/teximg/4/2/00388224.png) . Dies ist klar, denn schließlich wollen wir alle Auswahlmöglichkeiten durchlaufen. . Dies ist klar, denn schließlich wollen wir alle Auswahlmöglichkeiten durchlaufen.
Es ergibt sich also insgesamt der Binomische Lehrsatz
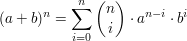 . .
Die 1. und 2. ((Binomische Formel))
Man sieht hieran auch, dass die erste und zweite binomische Formel nur ein Spezialfall für 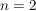 ist: ist:
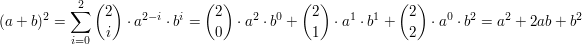 . .
Für die zweite Binomische Formel gilt Analoges, nur mit dem Unterschied, dass 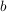 ein anderes Vorzeichen hat, was sich allerdings wegen des Quadrates in Glied 1 und 3 nur im 2. bemerkbar macht: ein anderes Vorzeichen hat, was sich allerdings wegen des Quadrates in Glied 1 und 3 nur im 2. bemerkbar macht:
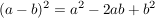
Häufig benötigt man auch diese Formel:
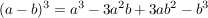
Die Koeffizienten ergeben sich aus dem ![Link auf "http://de.wikipedia.org/wiki/Pascalsches_Dreieck" [link]](/images/popup.gif) Pascalschen Dreieck. Pascalschen Dreieck.
|