direktes Produkt von HalbgruppenDefinition direktes Produkt von Halbgruppen
Schule
Universität
Es sei  eine nichtleere Menge und eine nichtleere Menge und 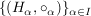 eine Familie von Halbgruppen. Auf dem mengentheoretischen direkten Produkt eine Familie von Halbgruppen. Auf dem mengentheoretischen direkten Produkt
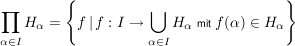
definieren wir eine innere Verknüpfun  durch durch
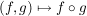 , ,
wobei 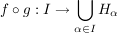 bestimmt ist durch bestimmt ist durch
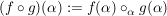 . .
Da die 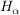 nicht leer sind, ist auch nicht leer sind, ist auch 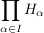 nicht leer (nach dem Auswahlaxiom) und da ferner alle nicht leer (nach dem Auswahlaxiom) und da ferner alle 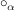 assoziativ sind, ist auch assoziativ sind, ist auch  assoziativ, denn assoziativ, denn
 = f(\alpha) \circ_{\alpha} g(\alpha) \circ_{\alpha} h(\alpha) = [f \circ (g \circ h)](\alpha) $ $ [(f \circ g) \circ h](\alpha) = f(\alpha) \circ_{\alpha} g(\alpha) \circ_{\alpha} h(\alpha) = [f \circ (g \circ h)](\alpha) $](/teximg/5/1/00387915.png) . .
Also ist 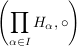 eine Halbgruppe, das direkte Produkt der Halgruppen eine Halbgruppe, das direkte Produkt der Halgruppen 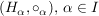 . .
Im Sonderfall 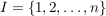 ist das ist das
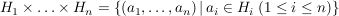
mit komponentenweiser Verknüpfung
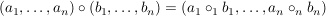 . .
Man beachte hier, dass die 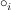 völlig verschiedene Verknüpfungen sein können, zum Beispiel im direkten Produkt von völlig verschiedene Verknüpfungen sein können, zum Beispiel im direkten Produkt von 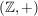 mit mit 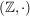 ist ist
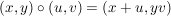 . .
Quelle: K. Meyberg, Algebra Teil 1, Carl Hanser Verlag, 1980, ISBN 3-446-13079-9
|