folgenstetig
Universität
Sei 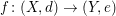 eine Abbildung zwischen metrischen Räumen. Ferner sei eine Abbildung zwischen metrischen Räumen. Ferner sei  Dann gilt: Dann gilt:
 ist genau dann folgenstetig in ist genau dann folgenstetig in 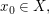 wenn für alle Folgen wenn für alle Folgen 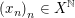 mit mit 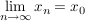 (d.h. (d.h. 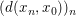 ist eine (reelle) Nullfolge) folgt, dass auch ist eine (reelle) Nullfolge) folgt, dass auch 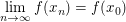 gilt (d.h. gilt (d.h. 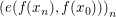 ist eine (reelle) Nullfolge). Bekanntlich ist eine solche Funktion genau dann stetig in ist eine (reelle) Nullfolge). Bekanntlich ist eine solche Funktion genau dann stetig in 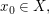 wenn wenn  folgenstetig in folgenstetig in  ist. Ferner ist eine Funktion ist. Ferner ist eine Funktion  genau dann stetig, wenn sie in allen genau dann stetig, wenn sie in allen  folgenstetig ist. folgenstetig ist.
Bemerkungen:
(1) Ist  ein isolierter Punkt, d.h. es gibt ein ein isolierter Punkt, d.h. es gibt ein 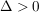 so, dass so, dass 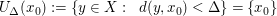 gilt, so ist gilt, so ist  stetig in stetig in 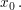
Beweis: Aus 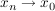 folgt die Existenz eines folgt die Existenz eines 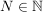 derart, dass derart, dass 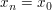 für alle für alle 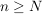 gilt (wähle etwa gilt (wähle etwa 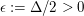 ). Wegen ). Wegen 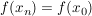 für alle für alle 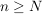 folgt dann schon folgt dann schon 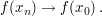 Also ist Also ist  folgenstetig in folgenstetig in  und damit insbesondere auch stetig in und damit insbesondere auch stetig in 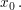 
(2) Die Funktion 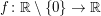 mit mit 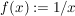 für für 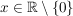 ist überall folgenstetig und damit auch überall stetig. Es macht keinen Sinn, die Funktion auf Stetigkeit an der Stelle ist überall folgenstetig und damit auch überall stetig. Es macht keinen Sinn, die Funktion auf Stetigkeit an der Stelle 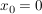 zu untersuchen, denn es ist zu untersuchen, denn es ist 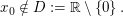
|