inversMatrizen invertieren
Um zu einer gegebenen Matrix A die inverse Matrix 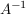 zu finden, zu finden,
löst man die Matrizengleichung  . .
Dabei ist 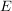 die Einheitsmatrix, die auf der Diagonalen 1 stehen hat und auf den anderen Plätzen 0: die Einheitsmatrix, die auf der Diagonalen 1 stehen hat und auf den anderen Plätzen 0:
 falls i=j, sonst falls i=j, sonst 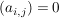 . .
X ist dann die inverse Matrix, die man mit 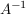 bezeichnet. bezeichnet.
Beispiel
Links die Ausgangsmatrix, rechts die Einheitsmatrix, und durch Zeilenumformungen links die Einheitsmatrix erzeugen, wobei rechts alle Schritte genau gleich mitgerechnet werden. In der Praxis, auf Papier, schreibt man allerdings die Matrixklammern nicht, sondern trennt die beiden Zahlenreihen einfach durch einen senkrechten Strich.
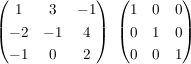
Jetzt kann man doch einfach das Doppelte der ersten Zeile zur zweiten addieren, und dann auch noch die erste Zeile zur dritten:

Um Brüche zu vermeiden, ist es vielleicht geschickt, zuerst die dritte Spalte zu bereinigen: addiere die dritte Zeile zur ersten, und auch das (-2)-fache der dritten Zeile zur zweiten:
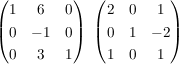
Jetzt noch das 6-fache der zweiten Zeile zur ersten addiert, das 3-fache der zweiten Zeile zur dritten:

Jetzt nur noch die mittlere Zeile mit (-1) multiplizieren:
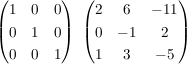
Nun kann man rechts die invertierte Matrix ablesen.
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Matrix_%28Mathematik%29#Die_inverse_Matrix" [link]](/images/popup.gif) Wikipedia Wikipedia
|