kartesischKartesisches Produkt
Das Kartesische Produkt  bezeichnet die Menge aller geordneten Paare bezeichnet die Menge aller geordneten Paare 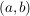 aus zwei nichtleeren Mengen aus zwei nichtleeren Mengen 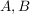 . Es gilt . Es gilt  und und 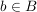 für alle Paare. für alle Paare.
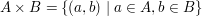
Falls 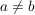 gilt gilt 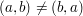
Beispiel
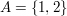 , , 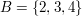
Dann ist
 . .
Das Kartesische Produkt kann im Übrigen auch für mehr als zwei und beliebig viele Mengen gebildet werden.
Seien 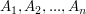 nichtleere Mengen, dann ist ihr Kartesisches Produkt nichtleere Mengen, dann ist ihr Kartesisches Produkt 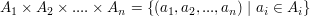 mit mit 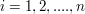 . .
Die Menge aller Punkte im kartesischen Koordinatensystem ist das Kartesische Produkt 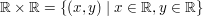
|