rationalDefinition rational
Schule
(Gebrochen-)rationale Funktion
Eine Funktion f heißt (gebrochen-)rationale Funktion, wenn sie als Quotient zweier ganzrationaler Funktionen g und h dargestellt werden kann:
Für jede rationale Funktion gilt:
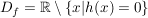 ,
d.h. die Nullstellen des Nenners gehören nicht zum Definitionsbereich,
man nennt sie auch Definitionslücken.
Offenbar ist die Menge der ganzrationalen Funktionen in der Menge der rationalen Funktionen enthalten.
Alle Funktionen, die sich nicht als Quotient zweier Polynome in x darstellen lassen, heißen nichtrationale Funktionen.
Universität
Die allgemeine Schreibweise lautet:
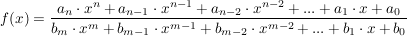
|