Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Analysis I/II
Vorkurs-Übungsaufgaben
| www.matheraum.de
Analysis
Aufgabenblatt 1
Abgabe: Mo 06.02.2012 10:00 | 30.01.2012 | | Die Übungsaufgaben beziehen sich auf das Inhaltsverzeichnis bzw. den Skriptverweis in der Kursbeschreibung. Die Aufgaben sind so angelegt, dass sie bequem in einer Woche gelöst werden können.
| | Die Aufgaben beziehen sich auf das Kapitel "Natürliche Zahlen/Vollständige Induktion" bzw. im Buch "Grundkurs Analysis 1" das Kapitel "Sprache der Analysis: 1.2 Induktion". Sie sollten vertraut sein mit: induktive Menge, Natürliche Zahlen, Vollständige Induktion, Summen- und Produktzeichen, Teleskopsumme, Binomialkoeffizient, Fakultät, Binomischer Lehrsatz, Summenformeln. | | Aufgabe 1 | Aufgabe I-1: Zeigen Sie mittels vollständiger Induktion die Bernoulli'sche Ungleichung:
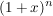 > 1 + nx für n > 1 + nx für n 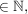 n n  2, x 2, x 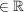 , x , x 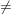 0, x > -1 0, x > -1 | | Aufgabe 2 | Aufgabe I-2: Für welche n 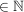 gilt die Aussage gilt die Aussage 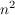 < < 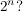 Beweisen Sie Ihre Vermutung durch vollständige Induktion! Beweisen Sie Ihre Vermutung durch vollständige Induktion! | | Aufgabe 3 | Aufgabe I-3: Beweisen Sie:
 - - 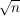 ) < ) < 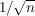 < <  - - 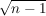 ) ) | | Aufgabe 4 | Aufgabe I-4: Berechnen Sie die Summe
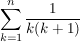
Hinweis: Teleskopsumme ! |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|