Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| Analysis I/II
Vorkurs-Übungsaufgaben
| www.matheraum.de
Analysis
Aufgabenblatt 2
Abgabe: Mo 13.02.2012 10:00 | 06.02.2012 | | Die Übungsaufgaben beziehen sich auf das Inhaltsverzeichnis bzw. den Skriptverweis in der Kursbeschreibung. Die Aufgaben sind so angelegt, dass sie bequem in einer Woche gelöst werden können.
| | Sie sollten für diesen Aufgabenzettel mit folgenden Begriffen vertraut sein: Fakultät, Permutation, Binomialkoeffizient, Binomischer Lehrsatz, Reelle Zahlen, (Absolut-)Betrag, Dreiecksungleichung, Arithmetische/Geometrisches Mittel, Schwartzsche Ungleichung, Intervall, Beschränktheit, Schranken, Grenze, Supremum, Infimum, Vollständigkeit, Satz von Archimedes, Gaußklammer | | Aufgabe 1 | II-1: Seien 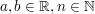 . Zeigen Sie die allgemeine binomische Formel: . Zeigen Sie die allgemeine binomische Formel:
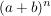 = = 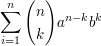 | | Aufgabe 2 | II-2:
a) Es seien die reellen Zahlen a,b gegeben mit |a-3| 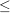 3 * 3 * 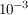 und |b+2| und |b+2| 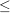 2 * 2 * 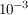 . Schätzen Sie damit (nach oben und unten) ab: . Schätzen Sie damit (nach oben und unten) ab:
|a+b-1|
b) Bestimmen Sie alle reellen Zahlen x, für die gilt:
||x+1|-|x+3||< 1 | | Aufgabe 3 | II-3: Seien x,y reelle Zahlen mit:
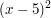 + + 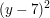 = 4 = 4
Zeigen Sie: 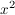 + + 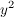 > 36 > 36
Hinweis: Überlegen Sie sich zunächst, welches geometrische Objekt damit auch beschrieben wird! (Skizze!) | | Aufgabe 4 | II-4: Untersuchen Sie, ob die Mengen M nach oben/unten beschränkt sind und bestimmen Sie ggf. sup M und inf M:
a) M := {x 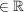 | x = 1 - | x = 1 - 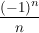 , n , n 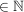 } }
b) M := {x 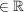 | x = t + | x = t +  , 0 < t , 0 < t 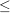 10, t 10, t 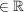 } } |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|