BasiswechselDer Basiswechsel
Beschreibung
gegeben sei ein Vektor eines Vektorraumes V mit der Darstellung v bzgl. der Basis A, d.h 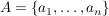 sei eine Basis, dann kann man sei eine Basis, dann kann man  eindeutig darstellen als Linearkombination der Basisvektoren, d.h : eindeutig darstellen als Linearkombination der Basisvektoren, d.h : 
somit erhält  die Darstellung bzgl die Darstellung bzgl 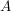 : : 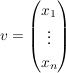
Wenn man nun eine weitere Basis 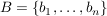 gegeben hat und den Vektor gleich (identisch) lassen, aber bzgl B (eindeutig) darstellen will, dann sind also die Skalare in gegeben hat und den Vektor gleich (identisch) lassen, aber bzgl B (eindeutig) darstellen will, dann sind also die Skalare in 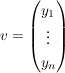 gesucht, so dass gesucht, so dass 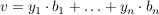 gilt. gilt.
Für allgemeine Basen kann man dies entweder über ein Gleichungssystem lösen - bzw. gleichbedeutend mit der Transformationsmatrix 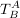 . .
Für eine orthogonale Basis B kann man auch das (kanonische) Skalarprodukt benutzen.
(für eine orthonormale Basis B entfallen jeweils die Nenner der Brüche)
Dann gilt : 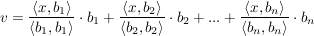
Für eine Herleitung und als Beispiel zur Berechnung nach den "beiden" anderen Methoden siehe ![Link auf "https://matheraum.de/read?t=124870" [link]](/images/popup.gif) HIER (Matheraum) HIER (Matheraum)
|