| Mach mit! und verbessere/erweitere diesen Artikel! | | Artikel • Seite bearbeiten • Versionen/Autoren | Dirac-MaßDefinition Dirac-Maß
Es seien
Dann heißt die Funktion
![$ \begin{array}{lccc} \varepsilon_\omega: & \mathcal{A} & \to & [0,+\infty] \\
&A & \mapsto & \begin{cases}1,\ \omega\in A\\0,\ \omega\not\in A\end{cases} \end{array} $](/teximg/3/3/00941033.png "$ \begin{array}{lccc} \varepsilon_\omega: & \mathcal{A} & \to & [0,+\infty] \\
&A & \mapsto & \begin{cases}1,\ \omega\in A\\0,\ \omega\not\in A\end{cases} \end{array} $")
das durch die Einheitsmasse in 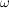 definierte Maß oder auch Dirac-Maß.
Siehe auch: Maß
Literatur: isbn3110136252
| | Erstellt: Mi 30.07.2008 von Marc | | Letzte Änderung: Mi 30.07.2008 um 13:16 von Marc | | | Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext |
|
