ExtremstelleExtremstelle einer Funktion
... heißt diejenige Zahl aus dem Definitionsbereich einer Funktion, für die die Funktion ein lokales Maximum oder Minimum hat.
Dabei kommt es nur darauf an, dass die Funktion in einer (kleinen) Umgebung der Extremstelle dort ein Maximum oder Minimum hat.
Extremstellen findet man bei differenzierbaren Funktionen als die Nullstellen der 1. Ableitung der Funktion, an denen die 2. Ableitung ungleich Null ist.
Ist  aus dem Definitionsbereich einer Funktion mit aus dem Definitionsbereich einer Funktion mit 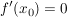 , so gilt: , so gilt:
-  ist eine Minimalstelle der Funktion, falls ist eine Minimalstelle der Funktion, falls 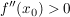 gilt gilt
-  ist eine Maximalstelle der Funktion, falls ist eine Maximalstelle der Funktion, falls 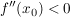 gilt gilt
Man sagt auch:
- Die Funktion hat an der Stelle
 eine (lokale oder relative) Maximalstelle, wenn die Funktion links von eine (lokale oder relative) Maximalstelle, wenn die Funktion links von  steigt, aber rechts von steigt, aber rechts von  fällt. fällt.
Der Punkt H( ; f( ; f( )) heißt in diesem Fall "(relativer) Hochpunkt". )) heißt in diesem Fall "(relativer) Hochpunkt".
Analog:
- Die Funktion hat an der Stelle
 eine (lokale oder relative) Minimalstelle, wenn die Funktion links von eine (lokale oder relative) Minimalstelle, wenn die Funktion links von  fällt, aber rechts von fällt, aber rechts von  steigt. steigt.
Der Punkt T( ; f( ; f( )) heißt in diesem Fall "(relativer) Tiefpunkt". )) heißt in diesem Fall "(relativer) Tiefpunkt".
Vorzeichenwechselkriterium:
- Die Funktion hat an der Stelle
 eine (lokale oder relative) Maximalstelle, wenn eine (lokale oder relative) Maximalstelle, wenn 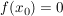 ist und ist und
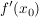 für zunehmende Werte von x in der Nähe von für zunehmende Werte von x in der Nähe von  von positiven zu negativen Werten wechselt. von positiven zu negativen Werten wechselt.
- Die Funktion hat an der Stelle
 eine (lokale oder relative) Minimalstelle, wenn eine (lokale oder relative) Minimalstelle, wenn 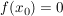 ist und ist und
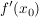 für zunehmende Werte von x in der Nähe von für zunehmende Werte von x in der Nähe von  von negativen zu positiven Werten wechselt. von negativen zu positiven Werten wechselt.
Für DIFFERENZIERBARE Funktionen gilt, dass es eine notwendige Bedingung ist, dass die 1. Ableitung an dem Extrempunkt 0 ist: f'( ) = 0. ) = 0.
Trifft dies zu und ist die 2. Ableitung ungleich null (f''( ) )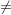 0), so ist die hinreichende Bedingung für einen lokalen Extrempunkt erfüllt. 0), so ist die hinreichende Bedingung für einen lokalen Extrempunkt erfüllt.
Ist die 1. Ableitung =0 und ebenfalls die 2. Ableitung, so kann trotzdem ein Extrempunkt vorhanden sein.
In diesem Fall sollte die Monotonie untersucht werden - was natürlich auch für eine Funktion gilt, die an der zu untersuchenden Stelle NICHT differenzierbar ist.
(Beispiel: Die Funktion mit der Gleichung y=|x| hat an der Stelle x=0 ein relatives Minimum, obwohl die Funktion dort NICHT differenzierbar ist!)
Daneben gibt es noch Randextrema.
Sie liegen immer dann vor, wenn eine Funktion an den Rändern ihres Definitionsbereichs einen höheren/kleineren Funktionswert hat als an den (lokalen) Extremstellen.
Der größte (kleinste) Funktionswert in einem Definitionsbereich ist zugleich das absolute (= globale) Maximum (Minimum).
siehe auch Kurvendiskussion
|