monotonMonotonie einer Funktion
Eine Funktion 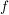 heißt "streng monoton steigend" auf dem Intervall heißt "streng monoton steigend" auf dem Intervall  , ,
wenn für alle 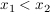 aus dem Intervall aus dem Intervall  gilt: gilt: 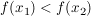 , ,
also: wenn für steigende  (aus (aus  ) auch die Funktionswerte steigen. ) auch die Funktionswerte steigen.
--
Eine Funktion 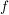 heißt "monoton steigend" auf dem Intervall heißt "monoton steigend" auf dem Intervall  , ,
wenn für alle 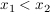 aus dem Intervall aus dem Intervall  gilt: gilt: 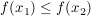 , ,
also: wenn für steigende  (aus (aus  ) die Funktionswerte nicht fallen. ) die Funktionswerte nicht fallen.
--
Analoge Definition für (streng) monoton fallende Funktion:
Eine Funktion 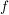 heißt "streng monoton fallend" auf dem Intervall heißt "streng monoton fallend" auf dem Intervall  , ,
wenn für alle 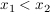 aus dem Intervall aus dem Intervall  gilt: gilt: 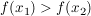 , ,
also: wenn für steigende  (aus (aus  ) die Funktionswerte fallen. ) die Funktionswerte fallen.
--
Eine Funktion 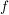 heißt "monoton fallend" auf dem Intervall heißt "monoton fallend" auf dem Intervall  , ,
wenn für alle 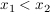 aus dem Intervall aus dem Intervall  gilt: gilt: 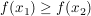 , ,
also: wenn für steigende  (aus (aus  ) die Funktionswerte nicht steigen. ) die Funktionswerte nicht steigen.
--
Voraussetzungen
Das Intervall 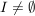 muß im Definitionsbereich der Funktion enthalten sein. muß im Definitionsbereich der Funktion enthalten sein.
Bemerkungen.
1.) Wenn die Funktion differenzierbar ist, ermittelt man oft zunächst die Extremstellen der Funktion, um Aussagen über das Monotonieverhalten der Funktion treffen zu können.
Es gilt nämlich (anschaulich):
Die Funktion "steigt" vom (lokalen) Tiefpunkt bis zum (lokalen) Hochpunkt, anschließend fällt sie wieder bis zum nächsten (lokalen) Tiefpunkt etc.
2.) Jede "streng monoton steigende" Funktion ist auch "monoton steigend".
3.) Jede "streng monoton fallende" Funktion ist auch "monoton fallend".
4.) Jede reellwertige monotone Funktion hat höchstens abzählbar viele Unstetigkeitsstellen, und diese sind alle Sprungstellen!
5.) Ist ![$ I=[a,b] \subset \IR $ $ I=[a,b] \subset \IR $](/teximg/9/0/00387709.png) ein Intervall und ist ein Intervall und ist 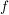 auf auf 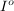 differenzierbar und stetig auf differenzierbar und stetig auf  , so gilt: , so gilt:
i) Genau dann, wenn 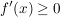 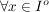 gilt, ist gilt, ist 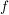 monoton wachsend auf monoton wachsend auf  . .
ii) Gilt 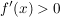 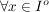 , so ist , so ist 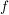 streng monoton wachsend auf streng monoton wachsend auf  . .
iii) Genau dann, wenn 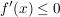 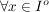 gilt, ist gilt, ist 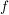 monoton fallend auf monoton fallend auf  . .
iv) Gilt  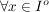 , so ist , so ist 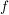 streng monoton fallend auf streng monoton fallend auf  . .
(Hierbei ist 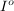 das Innere von das Innere von  , also , also 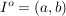 . Beweisen kann man die Aussagen 5.) i) bis iv) mit dem Mittelwertsatz.) . Beweisen kann man die Aussagen 5.) i) bis iv) mit dem Mittelwertsatz.)
Man beachte:
Z.B. 5.) ii) läßt sich nicht umkehren, d.h., unter den gegebenen Voraussetzungen an 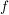 gilt: gilt:
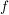 streng monoton auf streng monoton auf  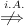 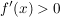 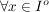 . .
Dazu betrachte man etwa 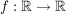 definiert durch definiert durch 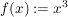 . . 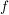 ist streng monoton auf ganz ist streng monoton auf ganz 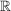 und differenzierbar auf ganz und differenzierbar auf ganz 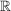 , also insbesondere stetig auf , also insbesondere stetig auf ![$ [-1,1] \subset \IR $ $ [-1,1] \subset \IR $](/teximg/7/1/00387717.png) und differenzierbar auf und differenzierbar auf 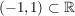 . Es gilt jedoch . Es gilt jedoch 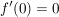 (und es ist (und es ist 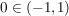 ). ).
Beispiele:
1.) Die Funktion 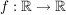 definiert durch definiert durch 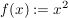 ist "(streng) monoton steigend" auf dem Intervall ist "(streng) monoton steigend" auf dem Intervall 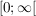 und "(streng) monoton fallend" auf dem Intervall und "(streng) monoton fallend" auf dem Intervall ![$ ]-\infty;0] $ $ ]-\infty;0] $](/teximg/5/3/00338735.png) . .
2.) Die Funktion 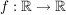 definiert durch definiert durch 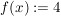 ist sowohl "monoton fallend" als auch "monoton steigend" auf jedem nichtleeren Intervall ist sowohl "monoton fallend" als auch "monoton steigend" auf jedem nichtleeren Intervall 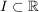 . .
Diese Funktion ist jedoch auf keinem Intervall 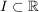 , das mehr als eine reelle Zahl enthält, "streng monoton (steigend oder fallend)". , das mehr als eine reelle Zahl enthält, "streng monoton (steigend oder fallend)".
3.) Die Funktion 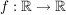 definiert durch definiert durch 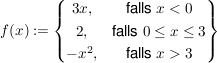
ist "streng monoton steigend" auf dem Intervall ![$ I_1:=]-\infty;0[ $ $ I_1:=]-\infty;0[ $](/teximg/2/2/00387722.png) , sowohl "monoton steigend" als auch "monoton fallend" auf dem Intervall , sowohl "monoton steigend" als auch "monoton fallend" auf dem Intervall ![$ I_2:=[0;3] $ $ I_2:=[0;3] $](/teximg/3/2/00387723.png) und "streng monoton fallend" auf dem Intervall und "streng monoton fallend" auf dem Intervall ![$ I_3:=]3;\infty[ $ $ I_3:=]3;\infty[ $](/teximg/4/2/00387724.png) . .
Ferner gilt hier:
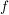 ist "monoton steigend" auf dem Intervall ist "monoton steigend" auf dem Intervall ![$ I_4:=I_1 \cup I_2=]-\infty;3] $ $ I_4:=I_1 \cup I_2=]-\infty;3] $](/teximg/5/2/00387725.png) (aber dort ist (aber dort ist 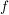 nicht streng monoton steigend!) und nicht streng monoton steigend!) und
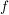 ist "monoton fallend" auf dem Intervall ist "monoton fallend" auf dem Intervall  (aber dort ist (aber dort ist 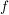 nicht streng monoton fallend!). nicht streng monoton fallend!).
|