Funktionen aus EigenschaftenGegeben ist im ersten Quadranten eine Fläche in Form eines Quadrates.
Gesucht ist die Gleichung der Parabel, die durch die beiden oberen Eckpunkte des
Quadrates P1 (0,4) und P2 (4,4) verläuft und das Quadrat in 2 flächengleiche Teile zerlegt.
Welche Bedingungen müssen die Koeffizienten b und c erfüllen,
damit die Funktion mit 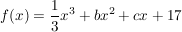 in keinem Punkt die Steigung 0 hat? in keinem Punkt die Steigung 0 hat?
Gesucht ist eine Funktion 3. Grades mit folgenden Eigenschaften:
- Punkt
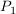 (1|1) Maximum, (1|1) Maximum,
- Punkt
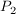 (3|f(3)) Wendepunkt, (3|f(3)) Wendepunkt,
- geht durch Nullpunkt des Koordinatensystems.
Eine Funktion 3. Ordnung
- hat in
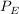 (4|0) einen Tiefpunkt, (4|0) einen Tiefpunkt,
- sie verläuft durch den Ursprung und durch den Punkt P (5|2,5).
Eine ganzrationale Funktion vierten Grades hat im Ursprung ein Extremum,
in P (-1|-3) besitzt sie einen Wendepunkt. Die zugehörige Wendetangente geht durch Q(0|2)!
Wie lautet die Funktionsgleichung?
Der Graph einer ganzrationalen Funktion 4. Grades hat im Wendepunkt W (2|0) eine horizontale Wendetangente. Die Normale im Ursprung des Koordinatensystems hat die Steigung  . .
Für jedes t > 0 ist eine Funktion 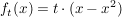
Ihr Schaubild sei 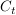 . Gib die Schnittpunkte von . Gib die Schnittpunkte von 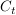 mit der x-Achse an. mit der x-Achse an.
Das Schaubild 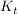 einer ganzrationalen Funktion einer ganzrationalen Funktion 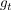 dritten Grades hat mit dritten Grades hat mit 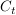 die Schnittpunkte mit der x-Achse gemeinsam. die Schnittpunkte mit der x-Achse gemeinsam.
Im linken Schnittpunkt berührt 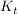 die Kurve die Kurve 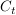 , ,
im rechten Schnittpunkt schneidet 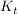 die Kurve die Kurve 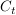 rechtwinklig. rechtwinklig.
Bestimme die Gleichung von 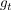 . .
siehe auch Funktion, Ortskurve, Funktionen aus Eigenschaften, Steckbriefaufgaben
Hinweis: zur Kontrolle sollte die Funktion stets gezeichnet werden, z. B. mit ![Link auf "http://www.funkyplot.de" [link]](/images/popup.gif) FunkyPlot. FunkyPlot.
|