Funktionsgrenzwert
Universität
Seien  und und 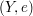 metrische Räume und sei metrische Räume und sei 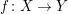 eine Funktion (zwischen den beiden metrischen Räumen; man schreibt dafür auch oft einfach eine Funktion (zwischen den beiden metrischen Räumen; man schreibt dafür auch oft einfach 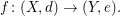 ). Sei ). Sei  ein Häufungspunkt (Menge) der Menge X. Die ein Häufungspunkt (Menge) der Menge X. Die 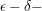 (besser: (besser: 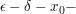 ) Definition des Begriffes Funktionsgrenzwert an der Stelle ) Definition des Begriffes Funktionsgrenzwert an der Stelle 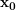 (siehe auch Grenzwert) lautet wie folgt: (siehe auch Grenzwert) lautet wie folgt:
Man sagt,  habe an der Stelle habe an der Stelle  einen Funktionsgrenzwert, wenn gilt: einen Funktionsgrenzwert, wenn gilt:
Es existiert ein 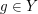 so, dass so, dass
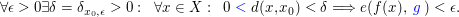
Falls ein 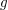 wie oben existiert, so schreibt man auch wie oben existiert, so schreibt man auch 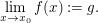 Man beachte dabei, dass das Symbol Man beachte dabei, dass das Symbol 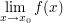 für den Funktionsgrenzwert von für den Funktionsgrenzwert von  an der Stelle an der Stelle  im Sinne von im Sinne von 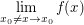 verwendet wird. Beachtenswert ist dabei insbesondere, dass weder verwendet wird. Beachtenswert ist dabei insbesondere, dass weder  an der Stelle an der Stelle  zu definiert sein braucht, noch, dass, falls zu definiert sein braucht, noch, dass, falls  gilt, auch gilt, auch 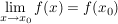 gelten muss. Falls allerdings gelten muss. Falls allerdings  gilt, so ist gilt, so ist  genau dann stetig in genau dann stetig in 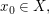 falls falls 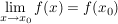 gilt. gilt.
Beispiel(e):
Betrachten wir
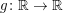
mit g(3):=2 und g(x):=1 für alle 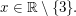 Ferner betrachten wir Ferner betrachten wir 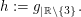
Dann gilt mit 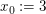 sowohl sowohl 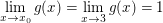 als auch als auch  obwohl zum einen obwohl zum einen 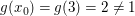 ist als auch zum anderen ist als auch zum anderen 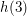 gar nicht existiert. gar nicht existiert.
Beweis:
Sei 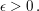 Sogar für jedes Sogar für jedes 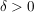 gilt: Für gilt: Für 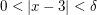 folgt (weil dann folgt (weil dann 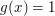 wegen wegen 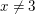 ist) ist)
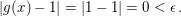
Analog auch:
Sei 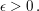 Sogar für jedes Sogar für jedes 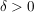 gilt: Für gilt: Für 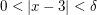 folgt (weil dann folgt (weil dann 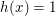 wegen wegen 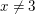 ist) ist)
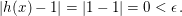

|