stetigDefinition stetig
Schule
Stetigkeit heißt im Prinzip nichts Anderes, als dass man den Graphen einer Funktion in ihrem Definitionsbereich ohne den Stift abzusetzen zeichnen kann. D.h. der Graph darf keine Sprünge machen (wie z.B. bei der Integer-Funktion). Das ist natürlich keine mathematisch exakte Definition, aber eine gute Veranschaulichung.
Mathematisch exakt lautet es in etwa so:
Die Funktion f ist an der Stelle 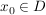 stetig, wenn stetig, wenn 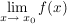 existiert und existiert und 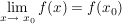
D.h. der (beidseitige!) Grenzwert muss existieren und dem Funktionswert an dieser Stelle entsprechen. Anschaulich: Wenn man sich von links der Stelle  nähert, muss man auf denselben Funktionswert kommen, wie wenn man sich ihr von rechts nähert UND der Wert muss gleich dem Funktionswert an dieser Stelle sein. nähert, muss man auf denselben Funktionswert kommen, wie wenn man sich ihr von rechts nähert UND der Wert muss gleich dem Funktionswert an dieser Stelle sein.
Eine Funktion ist stetig, wenn sie an allen Stellen ihres Definitionsbereiches stetig ist.
Zwei Beispiele für stetige Funktionen:
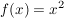
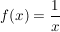
Und für eine unstetige Funktion:
![$ f(x)= [x] $ $ f(x)= [x] $](/teximg/8/6/00481568.png)
Universität
Seien  und und 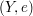 metrische Räume und sei metrische Räume und sei 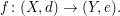 Sei Sei  Man sagt, dass Man sagt, dass  stetig in stetig in  ist, wenn der Funktionsgrenzwert ist, wenn der Funktionsgrenzwert 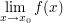 existiert und zudem existiert und zudem  gilt. Es ist also gilt. Es ist also  genau dann stetig in genau dann stetig in 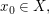 wenn: wenn:
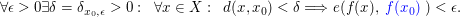
Ist  nicht stetig in nicht stetig in 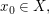 so sagt man, dass so sagt man, dass  unstetig in unstetig in  sei. sei.
Ferner heißt  (kurz) stetig, wenn (kurz) stetig, wenn  stetig in allen stetig in allen 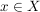 ist. Folglich ist ist. Folglich ist  genau dann unstetig, wenn es ein genau dann unstetig, wenn es ein  so gibt, dass so gibt, dass  unstetig in unstetig in  ist! ist!
Bemerkungen:
(1) Man beachte, dass es nur sinnvoll ist, eine Funktion an Stellen ihres Definitionsbereichs auf (Un-)Stetigkeit zu untersuchen!
(2) In metrischen Räumen ist der Begriff der Stetigkeit äquivlalent zu dem Begriff der Folgenstetigkeit.
|