GeradengleichungFormen der Geradengleichung
zunächst zweidimensional: im 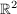
allgemeine Form der Geradengleichung
Dabei werden mit  die Werte auf der 1. Achse ( die Werte auf der 1. Achse ( -Achse) und mit -Achse) und mit 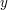 die Werte auf der 2. Achse ( die Werte auf der 2. Achse (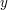 -Achse) bezeichnet; -Achse) bezeichnet; 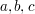 sind beliebige reelle Zahlen. sind beliebige reelle Zahlen.
Löst man diese Gleichung nach 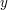 auf, so entsteht die Normalform: auf, so entsteht die Normalform:
Normalform
bekannt: die Steigung  der Geraden und ihr Achsenabschnitt der Geraden und ihr Achsenabschnitt  : :
Zwei-Punkte-Form
bekannt: zwei Punkte 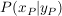 und und 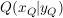 , die die Gerade festlegen: , die die Gerade festlegen:
Punkt-Steigungs-Form
bekannt: ein Punkt 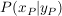 und die Steigung und die Steigung  der Geraden: der Geraden:
Bemerkung
als Merkregel kann gelten:
Durch "Abdecken" eines Teils der Doppelgleichung erhält man die oben stehenden Formeln.
Abschnittsform
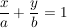 , ,
wobei  dem dem  -Achsenabschnitt (= Nullstelle) und -Achsenabschnitt (= Nullstelle) und 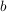 dem dem 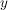 -Achsenabschnitt entspricht. -Achsenabschnitt entspricht.
und nun dreidimensional: im 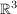
- entspricht der Punkt-Steigungs-Form (siehe oben)
- Hesse'sche Normalenform
- Achsenabschnittsform
- entspricht der allgemeinen Form (siehe oben)
|