InhaltDefinition Inhalt
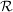 Ring in Ring in 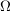 , , ![$ \mu:\ \mathcal{R}\to[0,+\infty] $ $ \mu:\ \mathcal{R}\to[0,+\infty] $](/teximg/8/5/00932458.png) Funktion. Funktion.
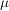 heißt Inhalt (auf heißt Inhalt (auf 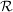 ) wenn ) wenn
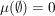 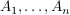 paarweise fremde Mengen paarweise fremde Mengen 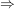 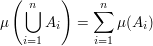 (endliche Additivität) (endliche Additivität)
Siehe auch: Prämaß, Maß
Weitere Eigenschaften:
(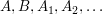 seien Mengen aus seien Mengen aus 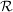 ) )
 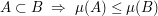 (Isotonie) (Isotonie)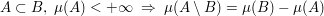 (Subtraktivität) (Subtraktivität)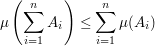 (Sub-Additivität) (Sub-Additivität)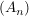 Folge paarweise fremder Mengen aus Folge paarweise fremder Mengen aus 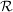 mit mit 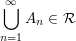 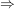 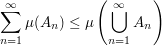
Beispiele:
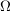 abzählbar-unendlich, abzählbar-unendlich, 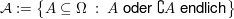 Algebra. Algebra. 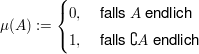 ist Inhalt (aber kein Prämaß). ist Inhalt (aber kein Prämaß).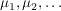 Folge von Inhalten (bzw. Prämaßen) auf Ring Folge von Inhalten (bzw. Prämaßen) auf Ring 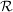 , , 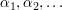 Folge nicht-negativer Zahlen. Folge nicht-negativer Zahlen. 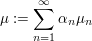 ist Inhalt (bzw. Prämaß) auf ist Inhalt (bzw. Prämaß) auf 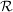
Attribute:
Ein Inhalt 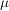 heißt... heißt...
- endlich
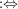  für alle für alle 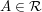
 -endlich -endlich 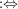 Es existiert Folge Es existiert Folge 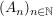 von Mengen aus von Mengen aus 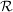 mit mit 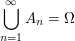 und und 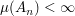 für alle für alle 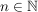
Literatur: isbn3110136252
|