PartiellIntegrationWie lerne ich die partielle Integration?
Also ich würde prinzipiell sagen: die Erfahrung macht's.
Es ist manchmal äusserst schwer erkennbar, was die Methode der Wahl ist.
Einen Hinweis kann ich dir aber geben: Prüfe, ob die Ableitung (bis auf einen Faktor a) der (potentiell) zu substituierenden Funktion wieder auftaucht, dann ist Substitution angezeigt.
Beispiel:
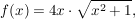
das hat die Gestalt: 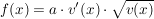 mit a=2 mit a=2
oder
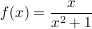
hat die Gestalt 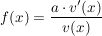 mit mit 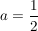
Klar?
Bei Funktionen, deren Ableitung/Stammfunktion identisch (bis auf einen Faktor) oder zyklisch (bis auf einen Faktor) sind, also bei der Form
 oder oder
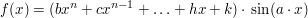 (oder cos) (oder cos)
ist immer partiell Integrieren angezeigt. Man setzt immer u=(...) und muss n-mal partiell integrieren, bis man am Ende ein Integral der Form
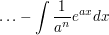 erhält, das man dann leicht nochmal integrieren kann. erhält, das man dann leicht nochmal integrieren kann.
Im Gegensatz dazu taucht z.B bei
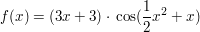
wieder die Ableitung der "inneren" (zu substituierenden Funktion) auf:
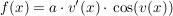 mit a=3 mit a=3
Auch bei
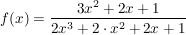
braucht man nicht mit Partialbruchzerlegung rummachen, wenn man erkennt, dass die Ableitung des Nenners bis auf einen Faktor im Zähler steht:
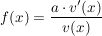 mit a=0,5 mit a=0,5
Bei manchen Funktionen muss man genauer hinsehen, z.B bei
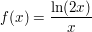
auch hier taucht die Ableitung auf:
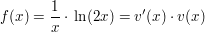
und wird am besten mit Substitution gelöst.
Ansonsten gilt: wer viel übt, hat viele Funktionen gesehen und entwickelt ein Gespür dafür.
Merke: Differenzieren ist ein Handwerk, Integrieren ist eine Kunst.
siehe Integrationsregel
|