TransversaleDefinition
Sei 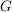 eine Gruppe und eine Gruppe und 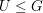 eine Untergruppe von eine Untergruppe von 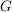 . . 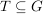 heißt Linkstransversale (Rechtstransversale) von heißt Linkstransversale (Rechtstransversale) von 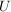 in in 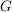 , ,
falls 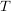 aus jeder Linksnebenklasse (Rechtsnebenklasse) von aus jeder Linksnebenklasse (Rechtsnebenklasse) von 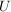 in in 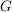 genau ein Element enthält. Offenbar gilt: genau ein Element enthält. Offenbar gilt:
Beispiel
Sei 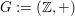 eine Gruppe und eine Gruppe und 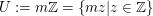 Untergruppe von Untergruppe von 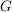 für ein für ein 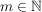 . .
Dann ist 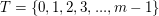 eine Transversale von eine Transversale von 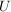 in in 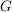 . .
Bemerkung
Der Begriff der Transversale wird insbesondere im Satz von Lagrange genutzt.
Man nennt die Rechts- oder Linkstransversale auch Repräsentantensystem der Rechts- bzw. Linksnebenklassen.
Literatur
isbn9783827430113 C. Karpfinger, K. Meyberg: Algebra, Springer Spektrum, 2013
|