UmkehrfunktionbestimmungGegeben sei die Funktion f mit
Die Funktion ist monoton steigend für 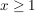 , weil der Scheitelpunkt bei (1|2) liegt. , weil der Scheitelpunkt bei (1|2) liegt.
Funktionen sind nur in ihrem Monotoniebereich umkehrbar! (Es könnte auch der andere Bereich sein.)
Daher ist sie für 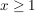 auch umkehrbar. auch umkehrbar.
Man vertauscht x und y: 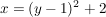
und löst nach y auf:
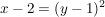 , Wurzel ziehen für , Wurzel ziehen für 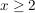 : :
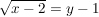
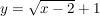 , fertig. , fertig.
Die Umkehrfunktion 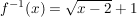 ist nur für ist nur für 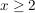 definiert! definiert!

|