unabhängig
Universität
Sei 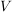 ein ein 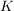 -Vektorraum. Sei für irgendeine Indexmenge -Vektorraum. Sei für irgendeine Indexmenge  nun nun 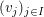 eine Familie von Elementen eine Familie von Elementen 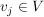 für alle für alle 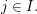 Man sagt, dass die Familie Man sagt, dass die Familie 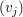 ( (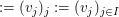 ) linear unabhängig sei, wenn für jede endliche Menge ) linear unabhängig sei, wenn für jede endliche Menge 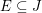 gilt: gilt:
Sind 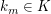 für alle für alle 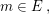 so gilt: so gilt:
Dabei ist 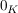 das additiv neutrale Element im Körper das additiv neutrale Element im Körper 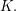
Familien, die nicht linear unabhängig sind, werden linear abhängig genannt.
Bemerkungen:
(1) Weil in 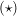 die Richtung die Richtung 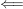 immer(!) gilt, kann man dort auch immer(!) gilt, kann man dort auch 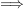 durch durch  ersetzen. ersetzen.
(2) Ist 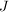 endlich, so ist endlich, so ist 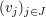 genau dann linear unabhängig, wenn genau dann linear unabhängig, wenn 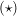 speziell für speziell für 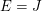 gilt. gilt.
Beweis. "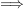 ": Ist trivial, weil ": Ist trivial, weil 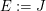 eine endliche Teilmenge von eine endliche Teilmenge von 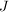 ist. ist.
"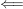 ": Man mache sich einfach klar, dass Teilfamilien linear unabhängiger Familien generell wieder linear unabhängig sein müssen. Dies wende man für den Spezialfall einer endlichen Familie an! ": Man mache sich einfach klar, dass Teilfamilien linear unabhängiger Familien generell wieder linear unabhängig sein müssen. Dies wende man für den Spezialfall einer endlichen Familie an!
(3) Ist 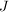 endlich, so sagt man oft auch einfach, dass die Vektoren endlich, so sagt man oft auch einfach, dass die Vektoren 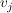 linear (un-)abhängig seien, wenn man meint, dass die Familie linear (un-)abhängig seien, wenn man meint, dass die Familie 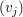 linear (un-)abhängig sei. linear (un-)abhängig sei.
(4) Um drei Vektoren 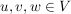 auf lineare Unabhängigkeit zu untersuchen, kann man folgenden kleinen Trick verwenden: auf lineare Unabhängigkeit zu untersuchen, kann man folgenden kleinen Trick verwenden:
Seien 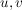 linear unabhängig. Genau dann sind linear unabhängig. Genau dann sind 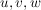 linear abhängig, wenn das GLS linear abhängig, wenn das GLS
lösbar in 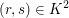 ist. ist.
Beweis. "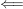 ": Sind ": Sind 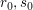 die Lösungen dieser Gleichung, so zeigt die Gleichung die Lösungen dieser Gleichung, so zeigt die Gleichung 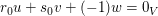 die lineare Abhängigkeit. die lineare Abhängigkeit.
"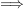 ": (Beweis per Kontraposition) Sei nun die Gleichung ": (Beweis per Kontraposition) Sei nun die Gleichung 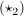 nicht lösbar. Angenommen, nicht lösbar. Angenommen, 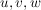 wären doch linear abhängig. Dann gibt es wären doch linear abhängig. Dann gibt es 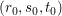 mit mit 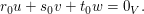 Wäre Wäre 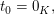 so folgte wegen der linearen Unabhängigkeit von so folgte wegen der linearen Unabhängigkeit von 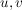 auch auch 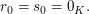 Dann wären Dann wären 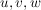 also doch linear unabhängig. Widerspruch. Also muss also doch linear unabhängig. Widerspruch. Also muss 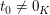 gelten. Dann folgt aber gelten. Dann folgt aber
so dass 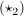 doch lösbar wäre, und zwar mit doch lösbar wäre, und zwar mit 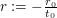 und und 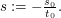 Widerspruch. Dies beendet den Beweis! Widerspruch. Dies beendet den Beweis! 
Beispiel:
Vorbemerkung:
In der Schule beschäftigt man sich meist mit der Frage, wann drei Vektoren 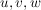 des des 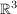 linear (un-)abhängig sind. Anstatt das GLS linear (un-)abhängig sind. Anstatt das GLS
in 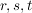 zu untersuchen. Hierbei helfen die Bemerkung (2) und (4) von oben: zu untersuchen. Hierbei helfen die Bemerkung (2) und (4) von oben:
Sind 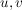 linear abhängig, so sind (siehe Hinweis zum Beweis in Bemerkung (2)) auch linear abhängig, so sind (siehe Hinweis zum Beweis in Bemerkung (2)) auch 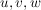 linear abhängig und wir haben nichts mehr zu rechnen. linear abhängig und wir haben nichts mehr zu rechnen.
Sind 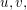 linear unabhängig, so betrachten wir das GLS in zwei Variablen: linear unabhängig, so betrachten wir das GLS in zwei Variablen:
Genau dann, wenn dieses nun lösbar in 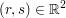 ist, ist dann ist, ist dann 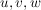 linear abhängig. D.h., wenn dieses nun nicht lösbar ist, sind die drei Vektoren linear abhängig. D.h., wenn dieses nun nicht lösbar ist, sind die drei Vektoren 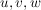 linear unabhängig. linear unabhängig.
Beispiele mit konkreten Vektoren:
(a) Seien 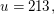 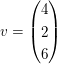 und und 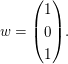 Wegen Wegen 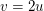 könnten wir direkt die lineare Abhängigkeit der drei Vektoren erkennen. Wir wenden aber trotzdem auch mal die Vorbemerkung in ungünstiger Weise an: könnten wir direkt die lineare Abhängigkeit der drei Vektoren erkennen. Wir wenden aber trotzdem auch mal die Vorbemerkung in ungünstiger Weise an:
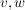 sind linear unabhängig. Betrachten wir nun also das GLS sind linear unabhängig. Betrachten wir nun also das GLS
Wir erhalten das GLS
(I) 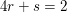
(II) 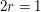
(III) 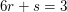
(II) ist gleichwertig zu 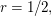 und setzen wir das in (I) ein, so folgt, dass diese gleichwertig ist zu und setzen wir das in (I) ein, so folgt, dass diese gleichwertig ist zu 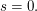 Weil damit auch (III) erfüllt ist, ist das GLS lösbar und die drei Vektoren sind linear abhängig. Weil damit auch (III) erfüllt ist, ist das GLS lösbar und die drei Vektoren sind linear abhängig.
(b) Seien 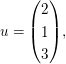 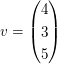 und und 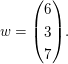 Offenbar sind Offenbar sind 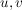 linear unabhängig. Das GLS linear unabhängig. Das GLS
geht über in
Daraus folgt das äquivalente GLS
(I) 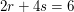
(II) 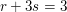
(III) 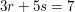
Aus (I)-2 (II) folgt (II) folgt 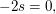 also also 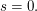 Damit ist Damit ist 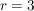 und (I) und (II) sind beide erfüllt. Setzen wir allerdings und (I) und (II) sind beide erfüllt. Setzen wir allerdings 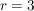 und und 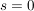 in (III)_ ein, so erhalten wir in (III)_ ein, so erhalten wir
Damit ist (III) nicht erfült, und das GLS, bestehend aus (I), (II) und (III), ist nicht lösbar in 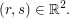 Folglich sind die drei obigen Vektoren Folglich sind die drei obigen Vektoren 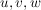 in unserem Teil (b) linear unabhängig. in unserem Teil (b) linear unabhängig.
Schule
Definition (linear) unabhängig (-e Vektoren)
Gegeben sei ein reeller (3-dimensionaler) Vektorraum, darin die Vektoren 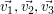 . .
Diese Vektoren heißen linear abhängig, wenn es Zahlen 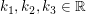 gibt mit: gibt mit:
wobei nicht alle k-Zahlen gleichzeitig Null sind.
anders gesagt: die Vektoren sind genau dann linear abhängig, wenn sich einer der Vektoren als Linearkombination der restlichen Vektoren ausdrücken lässt.
(Man beachte, dass man dabei nicht sagen darf, dass sich jeder der Vektoren als Linearkombination der anderen ausdrücken läßt. Dazu ein einfaches Beispiel: Sind 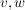 linear unabhängig und ist linear unabhängig und ist 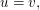 so kann eine Linearkombination von so kann eine Linearkombination von 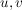 niemals den Vektor niemals den Vektor 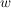 ergeben - denn andernfalls müßte ergeben - denn andernfalls müßte 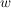 linear abhängig von linear abhängig von  sein!) sein!)
Vektoren, die nicht linear abhängig sind, nennt man linear unabhängig.
Anwendung:
Die Vektoren 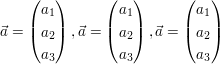 sind genau dann linear unabhängig, wenn sich ihre Linearkombination sind genau dann linear unabhängig, wenn sich ihre Linearkombination
nur für 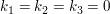 zum Vektor zum Vektor 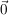 addiert. addiert.
Sind zwei Vektoren linear abhängig, so sind sie parallel und man nennt sie auch kollinear.
Sind drei Vektorne linear abhängig, so liegen sie in einer Ebene und man nennt sie auch komplanar.
siehe ![Link auf "http://de.wikipedia.org/wiki/Lineare_Unabh%C3%A4ngigkeit" [link]](/images/popup.gif) Wikipedia Wikipedia
|