MengeDefinition Menge
Zahlen oder andere unterscheidbare Objekte werden in der Mathematik zu einer Menge zusammengefasst.
Beispiele
aufzählende Form: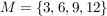
beschreibende Form: 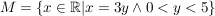
Definition Teilmenge
Werden aus einer Menge 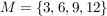 einige Elemente zu einer neuen Menge einige Elemente zu einer neuen Menge 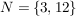 zusammengefasst, so nennt man N eine Teilmenge von M und schreibt: zusammengefasst, so nennt man N eine Teilmenge von M und schreibt: 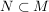 . .
Die leere Menge ist per Definition stets Teilmenge jeder anderen Menge: 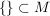 . .
Jede Menge ist aber auch Teilmenge von sich selbst: 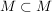 . .
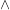 bedeutet: "und zugleich" bedeutet: "und zugleich"
Bezeichnung
Die Menge, die kein Element enthält heißt leere Menge und wird mit 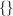 oder mit oder mit 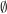 bezeichnet. bezeichnet.
Durchschnitt
Unter dem Durchschnitt (der Schnittmenge) von zwei Mengen versteht man die Menge der Elemente, die in beiden Mengen zugleich enthalten sind (in A und B):
Seien 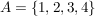 und und 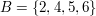 gegeben, dann ist gegeben, dann ist 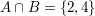 der Durchschnitt (die Schnittmenge) der beiden Mengen. der Durchschnitt (die Schnittmenge) der beiden Mengen.
Vereinigung
Unter der Vereinigung von zwei Mengen versteht man die Menge der Elemente, die in (mind.) einer der beiden Mengen enthalten sind (in A oder B):
Seien 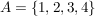 und und 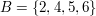 gegeben, dann ist gegeben, dann ist 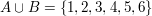 der Vereinigung der beiden Mengen. der Vereinigung der beiden Mengen.
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Menge_(Mathematik)" [link]](/images/popup.gif) Wikipedia Wikipedia
Universität
Naive Betrachtungen:
Es werden im allgemeinen mit großen Buchstaben 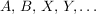 Mengen und mit kleinen Buchstaben Mengen und mit kleinen Buchstaben 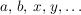 Elemente aus Mengen bezeichnet. Eine endliche Menge A wird vorzugsweise durch Angabe aller ihrer Elemente beschrieben, Elemente aus Mengen bezeichnet. Eine endliche Menge A wird vorzugsweise durch Angabe aller ihrer Elemente beschrieben, 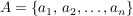 . Sehr üblich ist auch die Charakterisierung einer Menge X durch Angabe einer Eigenschaft E, die genau allen Elementen von X zukommt, . Sehr üblich ist auch die Charakterisierung einer Menge X durch Angabe einer Eigenschaft E, die genau allen Elementen von X zukommt,
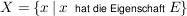
Die leere Menge wird mit 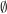 bezeichnet. bezeichnet.
Ist ein Objekt x Element einer Menge A (kürzer: x ist in A, bzw. x ist aus A), dann bezeichnen wir das durch 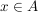 , gelegentlich auch , gelegentlich auch 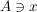 . Andernfalls, also wenn x nicht in A ist, schreiben wir . Andernfalls, also wenn x nicht in A ist, schreiben wir 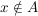 . .
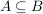 bedeutet, dass A eine Teilmenge von B ist, d.h. jedes x aus A ist auch in B. bedeutet, dass A eine Teilmenge von B ist, d.h. jedes x aus A ist auch in B. 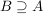 bedeutet dasselbe wie bedeutet dasselbe wie 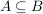 . .
Die Gleichheit von Mengen, A=B, ist durch 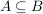 und und 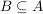 definiert. Um also A=B nachzuweisen, ist stets zu zeigen: definiert. Um also A=B nachzuweisen, ist stets zu zeigen: 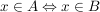 . .
Ist A eine echte Teilmenge von B, d.h. 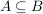 , aber , aber 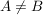 , dann kennzeichnen wir das durch , dann kennzeichnen wir das durch 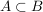 . Man achte sorgfältig auf den Unterschied der Zeichen . Man achte sorgfältig auf den Unterschied der Zeichen 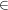 , , 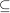 und und 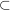 . Es ist . Es ist 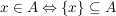 , außerdem ist bei , außerdem ist bei 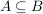 durchaus A=B möglich, bei durchaus A=B möglich, bei 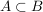 gibt es ein gibt es ein 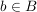 , das nicht in A liegt, , das nicht in A liegt, 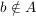 . .
Natürlich können auch Mengen als Elemente in einer Menge vorkommen, so in der Potenzmenge P(A) einer Menge A. Es ist
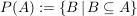 . .
Ist 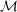 eine Menge von Mengen, dann bezeichnen wir den Durchschnitt alles Mengen aus eine Menge von Mengen, dann bezeichnen wir den Durchschnitt alles Mengen aus 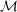 mit mit
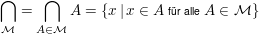 . .
Entsprechend für die Vereinigung
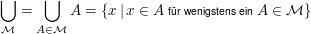 . .
Ist 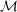 endlich, endlich, 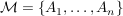 , dann sind auch die Bezeichnungen , dann sind auch die Bezeichnungen 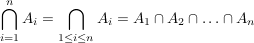 üblich. Für die Vereinigung gilt das analog. üblich. Für die Vereinigung gilt das analog.
Im Falle 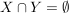 heißen X und Y disjunkt. heißen X und Y disjunkt.
Als relatives Komplement von B in A wird die Menge
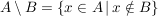
bezeichnet.
Das direkte oder cartesische Produkt der Mengen 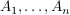 ist ist
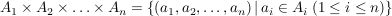 , ,
wobei darauf zu achten ist, dass 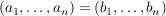 genau dann gilt, wenn genau dann gilt, wenn 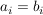 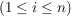 . .
Falls 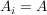 gilt für alle i gilt für alle i 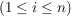 , dann schreiben wir für das Produkt auch , dann schreiben wir für das Produkt auch 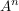
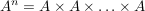 (n Faktoren). (n Faktoren).
Die Mächtigkeit einer Menge A wird mir 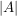 bezeichnet. Also bezeichnet. Also 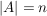 , wenn A aus n (verschiedenen) Elementen besteht. , wenn A aus n (verschiedenen) Elementen besteht.
Es ist
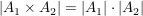 , ,
und für die Potenzmenge P(A) von A gilt:
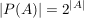 . .
Für die Menge der natürlichen Zahlen (ohne Null), natürlichen Zahlen zusammen mit der Null, ganzen Zahlen, rationalen Zahlen, reellen Zahlen und komplexen Zahlen werden die folgenden Standardbezeichnungen verwendet:
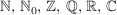 . .
Quelle: isbn3446130799
Attribute von Mengen:
abgeschlossen
abzählbar
beschränkt
dicht
endlich
leer
kompakt
messbar: Wenn sie in der Sigma-Algebra eines Messraumes enthalten ist.
offen
perfekt: Eine Teilmenge von 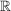 heißt perfekt, wenn sie gleich der Menge ihrer Häufungspunkte ist. heißt perfekt, wenn sie gleich der Menge ihrer Häufungspunkte ist.
überabzählbar: nicht abzählbar
unendlich
zusammenhängend
|